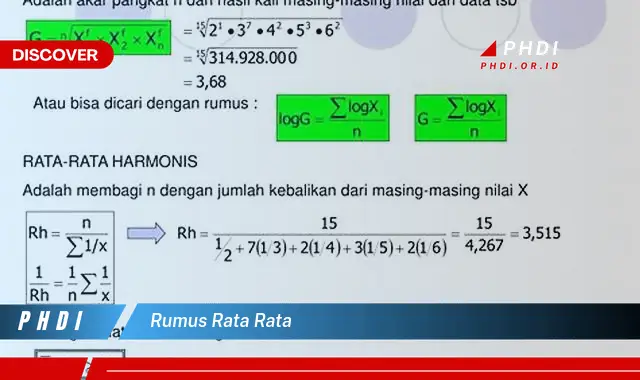
Rumus rata-rata adalah sebuah metode matematika untuk menghitung nilai rata-rata dari sekumpulan data. Rumus ini dihitung dengan menjumlahkan semua data dan membaginya dengan banyaknya data.
Rumus rata-rata sangat penting dalam statistik dan banyak digunakan dalam berbagai bidang, seperti penelitian, bisnis, dan pendidikan. Rumus ini memberikan informasi yang berguna tentang kecenderungan data dan dapat membantu dalam membuat keputusan atau prediksi.
Secara historis, konsep rata-rata telah digunakan sejak zaman kuno. Pada abad ke-17, ilmuwan seperti Christiaan Huygens dan Jakob Bernoulli mengembangkan teori probabilitas dan statistik, yang mencakup konsep rata-rata.
Rumus Rata-Rata
Rumus rata-rata adalah metode matematika penting yang digunakan untuk menghitung nilai rata-rata dari sekumpulan data. Rumus ini sangat penting dalam statistik dan memiliki berbagai aplikasi dalam penelitian, bisnis, dan pendidikan.
- Pengertian: Menjumlahkan semua data dan membaginya dengan banyaknya data.
- Jenis: Rata-rata hitung, rata-rata modus, rata-rata median.
- Tujuan: Memberikan informasi tentang kecenderungan data.
- Manfaat: Membantu dalam pengambilan keputusan dan prediksi.
- Sejarah: Digunakan sejak zaman kuno, dikembangkan oleh Huygens dan Bernoulli.
- Aplikasi: Bidang penelitian, bisnis, pendidikan, dan lainnya.
- Contoh: Menghitung nilai rata-rata ujian mahasiswa, menghitung rata-rata penjualan bulanan.
Dengan memahami konsep dan aplikasi rumus rata-rata, kita dapat memperoleh wawasan yang berharga dari sekumpulan data. Rumus ini memberikan dasar untuk analisis statistik yang lebih kompleks dan membantu kita membuat keputusan yang lebih tepat berdasarkan informasi.
Pengertian
Konsep menjumlahkan semua data dan membaginya dengan banyaknya data merupakan dasar dari rumus rata-rata. Proses ini memungkinkan kita untuk menghitung nilai rata-rata dari sekumpulan data, yang memberikan informasi penting tentang kecenderungan data tersebut.
- Komponen Rumus Rata-Rata: Menjumlahkan semua data dan membaginya dengan banyaknya data adalah dua komponen utama dari rumus rata-rata. Komponen-komponen ini mewakili proses menghitung total nilai data dan kemudian membaginya dengan jumlah data untuk mendapatkan nilai rata-rata.
- Aplikasi Praktis: Rumus rata-rata digunakan dalam berbagai aplikasi praktis, seperti menghitung nilai rata-rata ujian siswa, menghitung pendapatan rata-rata karyawan, atau menghitung rata-rata penjualan produk. Dalam setiap kasus, rumus ini memberikan informasi yang berguna tentang kecenderungan data.
- Interpretasi Hasil: Nilai rata-rata yang dihasilkan oleh rumus rata-rata dapat diinterpretasikan sebagai nilai tengah atau nilai khas dari sekumpulan data. Nilai ini dapat digunakan untuk membandingkan kumpulan data yang berbeda atau untuk mengidentifikasi pola dan tren dalam data.
- Keterbatasan: Meskipun rumus rata-rata adalah alat yang ampuh, namun memiliki keterbatasan. Misalnya, rumus ini dapat dipengaruhi oleh nilai ekstrem atau pencilan dalam data. Akibatnya, penting untuk mempertimbangkan jenis data dan distribusi data saat menggunakan rumus rata-rata.
Dengan memahami konsep dasar menjumlahkan semua data dan membaginya dengan banyaknya data, kita dapat menggunakan rumus rata-rata secara efektif untuk menganalisis kumpulan data yang berbeda. Rumus ini memberikan dasar untuk analisis statistik yang lebih kompleks dan membantu kita membuat keputusan yang lebih tepat berdasarkan informasi.
Jenis
Rumus rata-rata memiliki beberapa jenis, yaitu rata-rata hitung, rata-rata modus, dan rata-rata median. Masing-masing jenis memiliki karakteristik dan kegunaan yang berbeda dalam konteks analisis data.
- Rata-rata Hitung: Merupakan jenis rata-rata yang paling umum digunakan. Dihitung dengan menjumlahkan semua data dan membaginya dengan banyaknya data. Rata-rata hitung memberikan nilai rata-rata yang mempertimbangkan semua nilai data.
- Rata-rata Modus: Merupakan nilai data yang paling sering muncul dalam suatu kumpulan data. Rata-rata modus tidak mempertimbangkan nilai ekstrem dan cocok digunakan untuk data kategorikal atau data dengan distribusi asimetris.
- Rata-rata Median: Merupakan nilai tengah dari suatu kumpulan data yang telah diurutkan. Rata-rata median tidak terpengaruh oleh nilai ekstrem dan memberikan nilai rata-rata yang lebih stabil dibandingkan rata-rata hitung.
Pemilihan jenis rumus rata-rata yang tepat bergantung pada jenis data dan tujuan analisis. Dengan memahami perbedaan dan kegunaan masing-masing jenis rata-rata, kita dapat memperoleh informasi yang lebih akurat dan bermakna dari kumpulan data yang dianalisis.
Tujuan
Rumus rata-rata berperan penting dalam memberikan informasi tentang kecenderungan data karena memberikan nilai representatif yang menunjukkan titik tengah atau nilai khas dari sekumpulan data. Nilai rata-rata ini dapat digunakan untuk membandingkan kumpulan data yang berbeda, mengidentifikasi pola, dan membuat prediksi.
- Menunjukkan Distribusi Data: Rata-rata dapat menunjukkan bagaimana data tersebar. Rata-rata yang tinggi menunjukkan bahwa data cenderung tersebar di sekitar nilai yang lebih tinggi, sedangkan rata-rata yang rendah menunjukkan bahwa data cenderung tersebar di sekitar nilai yang lebih rendah.
- Mengidentifikasi Pola: Rata-rata dapat membantu mengidentifikasi pola dalam data. Misalnya, rata-rata penjualan bulanan selama beberapa tahun dapat menunjukkan tren musiman atau siklus bisnis.
- Membuat Prediksi: Rata-rata dapat digunakan untuk membuat prediksi tentang nilai data di masa depan. Misalnya, rata-rata nilai ujian siswa selama beberapa semester dapat digunakan untuk memprediksi nilai ujian mereka di semester berikutnya.
- Mengambil Keputusan: Rata-rata dapat membantu mengambil keputusan berdasarkan informasi. Misalnya, rata-rata tingkat kepuasan pelanggan dapat digunakan untuk memutuskan apakah perlu melakukan perubahan pada produk atau layanan.
Dengan memberikan informasi tentang kecenderungan data, rumus rata-rata merupakan alat penting untuk menganalisis data, mengidentifikasi pola, dan membuat keputusan yang tepat.
Manfaat
Rumus rata-rata memiliki peran penting dalam membantu pengambilan keputusan dan prediksi karena memberikan informasi tentang kecenderungan data. Dengan memahami nilai rata-rata, kita dapat memperoleh wawasan yang berharga yang dapat digunakan untuk mengambil keputusan yang lebih tepat dan membuat prediksi yang lebih akurat.
- Pengambilan Keputusan: Nilai rata-rata dapat digunakan sebagai dasar untuk mengambil keputusan yang berkaitan dengan berbagai aspek. Misalnya, rata-rata nilai ujian siswa dapat digunakan untuk memutuskan apakah siswa tersebut perlu mengikuti les tambahan. Rata-rata tingkat kepuasan pelanggan dapat digunakan untuk memutuskan apakah perlu melakukan perubahan pada produk atau layanan.
- Prediksi: Rumus rata-rata dapat digunakan untuk memprediksi nilai data di masa depan. Misalnya, rata-rata penjualan bulanan selama beberapa tahun dapat digunakan untuk memprediksi penjualan di bulan-bulan mendatang. Rata-rata suhu harian selama beberapa minggu dapat digunakan untuk memprediksi suhu di minggu-minggu mendatang.
Dengan demikian, rumus rata-rata merupakan alat yang ampuh untuk menganalisis data, membantu pengambilan keputusan, dan membuat prediksi. Dengan memahami cara menggunakan rumus rata-rata secara efektif, kita dapat memperoleh manfaat maksimal dari data yang kita miliki.
Sejarah
Sejarah panjang rumus rata-rata menunjukkan pentingnya dan relevansinya dalam analisis data. Sejak zaman kuno, konsep rata-rata telah digunakan untuk memahami kecenderungan data dan membuat keputusan.
- Penggunaan Awal: Rata-rata telah digunakan sejak zaman Mesir dan Babilonia untuk menghitung hasil panen dan pajak. Konsep ini kemudian dikembangkan lebih lanjut oleh matematikawan Yunani seperti Archimedes dan Eratosthenes.
- Pengembangan Teoretis: Pada abad ke-17, Christiaan Huygens dan Jakob Bernoulli memberikan kontribusi signifikan terhadap teori probabilitas dan statistik, yang mencakup konsep rata-rata. Mereka mengembangkan metode untuk menghitung rata-rata dari sekumpulan data dan membuktikan sifat-sifat rata-rata.
- Penggunaan Modern: Rumus rata-rata yang kita gunakan saat ini didasarkan pada pengembangan historis ini. Rumus ini telah menjadi alat yang sangat penting dalam berbagai bidang, termasuk penelitian, bisnis, dan pendidikan.
Dengan memahami sejarah rumus rata-rata, kita dapat mengapresiasi pentingnya dan keandalannya sebagai alat untuk menganalisis data dan memperoleh wawasan yang berharga.
Aplikasi
Rumus rata-rata memiliki relevansi dan aplikasi yang luas di berbagai bidang, termasuk penelitian, bisnis, pendidikan, dan lainnya.
- Penelitian: Dalam penelitian, rumus rata-rata digunakan untuk menganalisis data yang dikumpulkan, menghitung ukuran tendensi sentral, dan membuat kesimpulan tentang populasi yang lebih luas. Misalnya, peneliti dapat menggunakan rumus rata-rata untuk menghitung nilai rata-rata skor tes atau tingkat kepuasan pelanggan.
- Bisnis: Di dunia bisnis, rumus rata-rata digunakan untuk menganalisis data penjualan, menghitung laba rata-rata, dan mengevaluasi kinerja karyawan. Misalnya, perusahaan dapat menggunakan rumus rata-rata untuk menghitung penjualan rata-rata per bulan atau tingkat konversi rata-rata untuk kampanye pemasaran.
- Pendidikan: Dalam pendidikan, rumus rata-rata digunakan untuk menghitung nilai rata-rata siswa, mengevaluasi efektivitas metode pengajaran, dan membuat keputusan tentang penempatan siswa. Misalnya, guru dapat menggunakan rumus rata-rata untuk menghitung nilai rata-rata kelas atau mengevaluasi kemajuan siswa dari waktu ke waktu.
Selain bidang-bidang yang disebutkan di atas, rumus rata-rata juga digunakan dalam berbagai disiplin ilmu lainnya, seperti keuangan, kesehatan, dan ilmu sosial. Melalui penerapannya yang luas, rumus rata-rata memainkan peran penting dalam membantu kita memahami dan menganalisis data, sehingga memungkinkan kita membuat keputusan yang tepat dan memperoleh wawasan yang berarti.
Contoh
Contoh-contoh ini menggambarkan peran penting rumus rata-rata dalam kehidupan nyata. Dengan menghitung nilai rata-rata, kita dapat memperoleh wawasan berharga dari berbagai jenis data, membantu kita membuat keputusan yang tepat dan memahami berbagai tren.
-
Menghitung Nilai Rata-rata Ujian Mahasiswa
Rumus rata-rata digunakan untuk menghitung nilai rata-rata ujian mahasiswa, memberikan gambaran umum tentang kinerja kelas dan mengidentifikasi siswa yang memerlukan dukungan tambahan. Nilai rata-rata ini juga dapat digunakan untuk membandingkan kinerja antar kelas atau semester.
-
Menghitung Rata-rata Penjualan Bulanan
Dalam dunia bisnis, rumus rata-rata digunakan untuk menghitung rata-rata penjualan bulanan, membantu perusahaan melacak kinerja penjualan, mengidentifikasi tren, dan membuat proyeksi untuk masa depan. Rata-rata penjualan bulanan juga dapat digunakan untuk membandingkan kinerja antar cabang atau periode waktu.
Dengan demikian, rumus rata-rata menjadi alat penting dalam berbagai bidang, memungkinkan kita menganalisis data, memahami tren, dan membuat keputusan berdasarkan informasi.
Pertanyaan Umum tentang Rumus Rata-Rata
Rumus rata-rata adalah alat yang sangat berguna untuk menganalisis data dan memperoleh informasi yang berharga. Berikut beberapa pertanyaan umum dan jawabannya untuk memberikan pemahaman yang lebih baik tentang rumus ini:
Pertanyaan 1: Apa itu rumus rata-rata dan bagaimana cara menghitungnya?
Jawaban: Rumus rata-rata adalah metode untuk menghitung nilai rata-rata dari sekumpulan data. Untuk menghitungnya, jumlahkan semua nilai data dan bagi dengan jumlah data.
Pertanyaan 2: Kapan rumus rata-rata harus digunakan?
Jawaban: Rumus rata-rata dapat digunakan ketika kita ingin mengetahui nilai rata-rata dari suatu kumpulan data, seperti nilai rata-rata ujian siswa atau rata-rata penjualan bulanan suatu perusahaan.
Pertanyaan 3: Apa saja jenis-jenis rumus rata-rata?
Jawaban: Ada beberapa jenis rumus rata-rata, seperti rata-rata hitung, rata-rata modus, dan rata-rata median. Masing-masing jenis memiliki kelebihan dan kekurangannya sendiri, tergantung pada jenis data dan tujuan analisis.
Pertanyaan 4: Apa saja manfaat menggunakan rumus rata-rata?
Jawaban: Rumus rata-rata memberikan informasi yang berharga tentang kecenderungan data, membantu dalam pengambilan keputusan, dan memungkinkan kita membuat prediksi yang lebih akurat.
Dengan memahami rumus rata-rata dan penggunaannya, kita dapat menganalisis data secara efektif dan memperoleh wawasan yang bermakna untuk berbagai tujuan.
Catatan: Untuk informasi lebih rinci tentang rumus rata-rata, silakan merujuk ke bagian selanjutnya dari artikel ini.
Tips Menggunakan Rumus Rata-Rata
Rumus rata-rata, meskipun merupakan konsep statistik dasar, memerlukan pemahaman yang baik untuk digunakan secara efektif. Berikut beberapa tips penting untuk menggunakan rumus rata-rata dengan benar:
Tips 1: Tentukan Jenis Rata-Rata yang Tepat
Ada beberapa jenis rata-rata, seperti rata-rata hitung, rata-rata modus, dan rata-rata median. Pilih jenis rata-rata yang paling sesuai dengan jenis data dan tujuan analisis Anda.
Tips 2: Periksa Pencilan
Perhatikan adanya nilai ekstrem atau pencilan dalam data Anda karena dapat memengaruhi nilai rata-rata. Pertimbangkan untuk menggunakan rata-rata median atau pendekatan lain untuk mengurangi dampak pencilan.
Tips 3: Pertimbangkan Distribusi Data
Pahami distribusi data Anda. Rumus rata-rata mungkin tidak sesuai untuk data yang sangat asimetris atau memiliki banyak pencilan.
Tips 4: Gunakan Kalkulator atau Perangkat Lunak
Untuk kumpulan data yang besar, gunakan kalkulator atau perangkat lunak statistik untuk menghitung rumus rata-rata guna menghindari kesalahan perhitungan manual.
Tips 5: Interpretasikan Hasil dengan Hati-hati
Nilai rata-rata harus diinterpretasikan dengan hati-hati karena dapat menyesatkan jika data tidak mewakili populasi yang lebih luas.
Dengan mengikuti tips ini, Anda dapat menggunakan rumus rata-rata secara efektif untuk menganalisis data dan memperoleh wawasan yang bermakna.
Kesimpulan
Rumus rata-rata adalah alat penting dalam statistik, tetapi penting untuk menggunakannya secara tepat untuk mendapatkan hasil yang akurat dan bermakna. Dengan mempertimbangkan jenis rata-rata, pencilan, distribusi data, dan interpretasi yang cermat, Anda dapat memanfaatkan rumus rata-rata untuk analisis data yang efektif.
Youtube Video:










