Rumus luas permukaan kubus adalah persamaan matematika yang digunakan untuk menghitung luas permukaan bangun ruang kubus. Rumus ini dapat digunakan untuk menghitung luas permukaan kubus dengan berbagai ukuran.
Rumus luas permukaan kubus sangat penting dalam berbagai bidang, seperti arsitektur, desain interior, dan teknik. Rumus ini juga dapat digunakan untuk menghitung volume kubus, karena luas permukaan kubus berhubungan dengan volumenya.
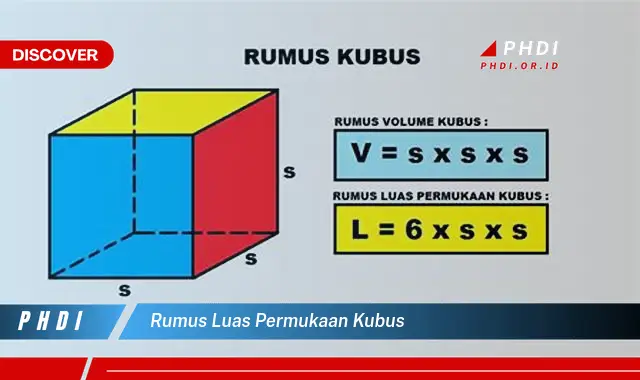
Rumus luas permukaan kubus adalah 6 x s, di mana s adalah panjang rusuk kubus. Misalnya, jika panjang rusuk kubus adalah 5 cm, maka luas permukaan kubus tersebut adalah 6 x 5 = 150 cm.
Rumus Luas Permukaan Kubus
Rumus luas permukaan kubus merupakan persamaan matematika yang penting dalam berbagai bidang, seperti arsitektur, desain interior, dan teknik. Rumus ini digunakan untuk menghitung luas permukaan bangun ruang kubus dengan berbagai ukuran.
- Rumus: 6 x s (di mana s adalah panjang rusuk kubus)
- Satuan: cm2, m2, atau sesuai dengan satuan panjang rusuk
- Konsep: Luas permukaan kubus adalah jumlah luas semua sisi kubus
- Aplikasi: Menghitung kebutuhan cat, wallpaper, atau bahan pelapis lainnya untuk kubus
- Keterkaitan: Luas permukaan kubus terkait dengan volumenya (V = s3)
- Sejarah: Rumus luas permukaan kubus telah dikenal sejak zaman kuno
- Contoh: Kubus dengan panjang rusuk 5 cm memiliki luas permukaan 150 cm2
Dengan memahami key aspects rumus luas permukaan kubus, kita dapat menyelesaikan berbagai permasalahan yang berkaitan dengan bangun ruang kubus, seperti menghitung kebutuhan bahan, merencanakan desain, atau memahami konsep geometri ruang.
Rumus
Rumus luas permukaan kubus, yaitu 6 x s, merupakan persamaan matematika yang diturunkan dari konsep dasar geometri ruang. Rumus ini menyatakan bahwa luas permukaan kubus sama dengan enam kali luas salah satu sisinya.
- Komponen: Rumus ini terdiri dari dua komponen, yaitu 6 (konstanta) dan s (panjang rusuk kubus).
- Contoh: Jika sebuah kubus memiliki panjang rusuk 5 cm, maka luas permukaan kubus tersebut adalah 6 x 5 = 150 cm2.
- Implikasi: Rumus ini menunjukkan bahwa luas permukaan kubus berbanding lurus dengan kuadrat panjang rusuknya. Artinya, jika panjang rusuk kubus diperbesar dua kali lipat, maka luas permukaannya akan menjadi empat kali lipat.
- Penerapan: Rumus luas permukaan kubus banyak digunakan dalam berbagai bidang, seperti arsitektur, desain interior, dan teknik, untuk menghitung kebutuhan bahan, merencanakan desain, atau memahami konsep geometri ruang.
Dengan memahami komponen, contoh, implikasi, dan penerapan rumus luas permukaan kubus, kita dapat memperoleh pemahaman yang komprehensif tentang bangun ruang kubus dan menyelesaikan berbagai permasalahan yang berkaitan dengannya.
Satuan
Dalam konteks rumus luas permukaan kubus, satuan yang digunakan untuk menyatakan luas permukaan adalah sesuai dengan satuan panjang rusuk kubus.
- Konsistensi Satuan: Penting untuk menggunakan satuan yang konsisten untuk panjang rusuk dan luas permukaan. Misalnya, jika panjang rusuk dinyatakan dalam sentimeter (cm), maka luas permukaan juga harus dinyatakan dalam sentimeter persegi (cm2).
- Konversi Satuan: Jika diperlukan, satuan panjang rusuk dan luas permukaan dapat dikonversi menggunakan faktor konversi yang sesuai. Misalnya, 1 meter (m) sama dengan 100 sentimeter (cm), sehingga 1 meter persegi (m2) sama dengan 10.000 sentimeter persegi (cm2).
- Implikasi Praktis: Pemilihan satuan yang tepat sangat penting dalam aplikasi praktis rumus luas permukaan kubus. Misalnya, dalam arsitektur, satuan meter persegi (m2) umumnya digunakan untuk menghitung luas permukaan bangunan, termasuk kubus.
Dengan memahami hubungan antara satuan panjang rusuk dan satuan luas permukaan, kita dapat memastikan penggunaan rumus luas permukaan kubus yang akurat dan konsisten, sehingga menghasilkan perhitungan yang tepat.
Konsep
Konsep ini merupakan landasan penting untuk memahami rumus luas permukaan kubus. Kubus memiliki enam sisi yang berbentuk persegi, dan masing-masing sisi memiliki luas yang sama.
- Perhitungan Luas Sisi: Untuk menghitung luas permukaan kubus, kita perlu terlebih dahulu menghitung luas salah satu sisinya. Luas persegi dihitung dengan mengalikan panjang sisinya dengan dirinya sendiri (s x s).
- Penjumlahan Luas Sisi: Setelah menghitung luas satu sisi, kita perlu menjumlahkannya dengan luas kelima sisi lainnya yang sama. Hal ini dikarenakan kubus memiliki enam sisi yang identik.
- Contoh: Misalkan sebuah kubus memiliki panjang rusuk 5 cm. Luas satu sisi kubus adalah 5 cm x 5 cm = 25 cm2. Luas permukaan kubus adalah 6 x 25 cm2 = 150 cm2.
- Implikasi: Konsep ini menunjukkan bahwa luas permukaan kubus berbanding lurus dengan kuadrat panjang rusuknya. Jika panjang rusuk suatu kubus diperbesar dua kali lipat, maka luas permukaannya akan menjadi empat kali lipat.
Dengan memahami konsep ini, kita dapat memahami bagaimana rumus luas permukaan kubus (6 x s) diturunkan dan bagaimana rumus tersebut digunakan untuk menghitung luas permukaan kubus dengan berbagai ukuran.
Aplikasi
Rumus luas permukaan kubus sangat penting dalam bidang seperti arsitektur, desain interior, dan teknik, salah satunya adalah untuk menghitung kebutuhan cat, wallpaper, atau bahan pelapis lainnya untuk kubus.
Mengetahui luas permukaan kubus sangat penting untuk menentukan jumlah bahan pelapis yang dibutuhkan. Dengan menggunakan rumus luas permukaan kubus, kita dapat menghitung luas setiap sisi kubus, kemudian menjumlahkannya untuk mendapatkan luas permukaan total.
Misalnya, sebuah kubus berukuran 5 cm x 5 cm x 5 cm. Luas permukaan kubus tersebut adalah 6 x (5 cm x 5 cm) = 150 cm2. Jika kita ingin mengecat kubus tersebut, maka kita membutuhkan cat dengan luas 150 cm2.
Selain untuk menghitung kebutuhan cat, rumus luas permukaan kubus juga dapat digunakan untuk menghitung kebutuhan wallpaper atau bahan pelapis lainnya. Dengan mengetahui luas permukaan kubus, kita dapat menentukan jumlah bahan yang dibutuhkan secara akurat, sehingga dapat meminimalkan pemborosan dan menghemat biaya.
Keterkaitan
Rumus luas permukaan kubus terkait erat dengan volumenya. Volume kubus dihitung dengan mengalikan panjang rusuknya (s) dengan dirinya sendiri tiga kali (s3).
- Perbandingan Luas Permukaan dan Volume: Terdapat hubungan yang jelas antara luas permukaan kubus dan volumenya. Luas permukaan sebuah kubus berbanding lurus dengan kuadrat panjang rusuknya (s2), sedangkan volumenya berbanding lurus dengan pangkat tiga panjang rusuknya (s3).
- Aplikasi Praktis: Keterkaitan ini memiliki aplikasi praktis dalam berbagai bidang. Misalnya, dalam teknik sipil, mengetahui volume dan luas permukaan kubus sangat penting untuk menghitung kebutuhan bahan dan biaya konstruksi.
- Contoh: Sebuah kubus dengan panjang rusuk 5 cm memiliki luas permukaan 150 cm2 dan volume 125 cm3. Hal ini menunjukkan hubungan yang jelas antara luas permukaan dan volume kubus.
Dengan memahami keterkaitan antara luas permukaan kubus dan volumenya, kita dapat memperoleh pemahaman yang lebih komprehensif tentang bangun ruang kubus dan hubungannya dengan konsep geometri ruang lainnya.
Sejarah
Rumus luas permukaan kubus, yang dinyatakan sebagai 6 x s, telah dikenal dan digunakan sejak zaman kuno. Hal ini menunjukkan bahwa konsep geometri dan pengukuran telah dipahami dan diaplikasikan oleh para ilmuwan dan matematikawan pada masa itu.
Pengetahuan tentang rumus luas permukaan kubus sangat penting dalam peradaban kuno, seperti Mesir dan Yunani. Bangsa Mesir menggunakannya dalam pembangunan piramida, yang merupakan struktur geometris kompleks yang membutuhkan perhitungan luas permukaan yang akurat. Sementara itu, para filsuf Yunani seperti Euclid dan Archimedes mengembangkan teorema dan prinsip geometri yang menjadi dasar bagi rumus luas permukaan kubus.
Dengan memahami sejarah rumus luas permukaan kubus, kita dapat mengapresiasi pentingnya ilmu pengetahuan dan matematika sepanjang sejarah. Rumus ini tidak hanya sekadar persamaan, tetapi juga merupakan bukti kecerdasan dan kemampuan manusia dalam memahami dan mengukur dunia di sekitar mereka.
Contoh
Contoh ini mengilustrasikan penerapan rumus luas permukaan kubus dalam konteks nyata. Dengan memberikan contoh spesifik, kita dapat memahami dengan lebih jelas bagaimana rumus tersebut digunakan dan ditafsirkan.
- Komponen Rumus: Contoh ini menunjukkan bahwa rumus luas permukaan kubus terdiri dari dua komponen: panjang rusuk (s) dan konstanta 6. Dalam contoh ini, s = 5 cm.
- Aplikasi Rumus: Untuk menghitung luas permukaan kubus, kita cukup mengalikan panjang rusuk dengan konstanta 6. Dalam contoh ini, 6 x 5 cm = 150 cm2.
- Interpretasi Hasil: Hasil perhitungan, 150 cm2, mewakili luas permukaan total kubus. Artinya, kita membutuhkan bahan seluas 150 cm2 untuk menutupi seluruh permukaan kubus.
Dengan memahami contoh spesifik ini, kita dapat memperoleh pemahaman yang lebih komprehensif tentang rumus luas permukaan kubus dan cara menggunakannya untuk menyelesaikan masalah praktis.
Pertanyaan Umum tentang Rumus Luas Permukaan Kubus
Bagian ini akan membahas beberapa pertanyaan umum dan kesalahpahaman mengenai rumus luas permukaan kubus.
Pertanyaan 1: Bagaimana cara menggunakan rumus luas permukaan kubus?
Jawaban: Rumus luas permukaan kubus adalah 6 x s, di mana s adalah panjang rusuk kubus. Untuk menggunakan rumus ini, cukup kalikan panjang rusuk dengan 6.
Pertanyaan 2: Apa satuan luas permukaan kubus?
Jawaban: Satuan luas permukaan kubus adalah satuan panjang rusuk kuadrat. Misalnya, jika panjang rusuk kubus dalam sentimeter, maka luas permukaannya dalam sentimeter persegi.
Pertanyaan 3: Apa kaitan antara luas permukaan kubus dan volumenya?
Jawaban: Luas permukaan kubus berbanding lurus dengan kuadrat panjang rusuknya, sedangkan volumenya berbanding lurus dengan pangkat tiga panjang rusuknya.
Pertanyaan 4: Kapan rumus luas permukaan kubus pertama kali ditemukan?
Jawaban: Rumus luas permukaan kubus telah dikenal sejak zaman kuno, sekitar 2000 tahun yang lalu.
Dengan memahami pertanyaan umum ini, kita dapat memperoleh pemahaman yang lebih komprehensif tentang rumus luas permukaan kubus dan penerapannya.
Ringkasan: Rumus luas permukaan kubus adalah alat penting dalam geometri dan memiliki berbagai aplikasi dalam kehidupan nyata. Memahami rumus ini dan cara menggunakannya sangat penting untuk menyelesaikan masalah yang berkaitan dengan bangun ruang kubus.
Transisi: Bagian selanjutnya akan membahas aplikasi praktis dari rumus luas permukaan kubus.
Tips Menggunakan Rumus Luas Permukaan Kubus
Rumus luas permukaan kubus sangat penting dalam berbagai bidang, seperti arsitektur, desain interior, dan teknik. Memahami cara menggunakan rumus ini dengan benar dapat membantu kita menyelesaikan masalah yang berkaitan dengan bangun ruang kubus secara efektif.
Tip 1: Pahami Konsep Dasar
Rumus luas permukaan kubus adalah 6 x s, di mana s adalah panjang rusuk kubus. Konsep dasar ini harus dipahami dengan jelas sebelum menggunakan rumus.
Tip 2: Pastikan Satuan yang Konsisten
Satuan panjang rusuk dan luas permukaan harus konsisten. Jika panjang rusuk dalam sentimeter, maka luas permukaan harus dalam sentimeter persegi.
Tip 3: Hitung Luas Satu Sisi Terlebih Dahulu
Luas permukaan kubus adalah jumlah luas keenam sisinya. Untuk itu, hitung luas satu sisi terlebih dahulu dengan mengalikan panjang rusuk dengan dirinya sendiri.
Tip 4: Gunakan Kalkulator untuk Akurasi
Penggunaan kalkulator dapat membantu memastikan akurasi perhitungan, terutama untuk kubus dengan panjang rusuk besar.
Tip 5: Visualisasikan Kubus
Memvisualisasikan kubus dapat membantu memahami bagaimana rumus diterapkan. Bayangkan kubus terbentang menjadi enam persegi, dan hitung luas totalnya.
Dengan mengikuti tips ini, kita dapat menggunakan rumus luas permukaan kubus dengan percaya diri dan efektif.
Kesimpulan:Rumus luas permukaan kubus adalah alat yang ampuh untuk menyelesaikan masalah yang berkaitan dengan bangun ruang kubus. Dengan memahami konsep dasar, memastikan satuan yang konsisten, dan mengikuti tips yang diberikan, kita dapat menggunakan rumus ini secara akurat dan efisien.
Youtube Video: