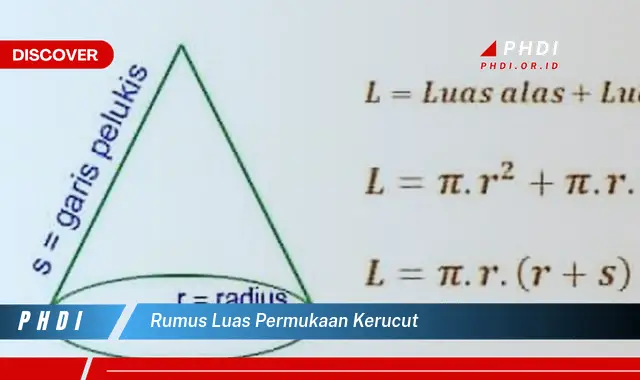
Rumus luas permukaan kerucut adalah persamaan matematika yang digunakan untuk menentukan luas permukaan kerucut. Luas permukaan kerucut terdiri dari luas alas yang berbentuk lingkaran dan luas selimut kerucut.
Rumus luas permukaan kerucut sangat penting dalam berbagai bidang, seperti teknik, arsitektur, dan desain. Rumus ini membantu para insinyur dan arsitek untuk menghitung jumlah bahan yang dibutuhkan untuk membuat kerucut, seperti lembaran logam atau kain. Selain itu, rumus ini juga digunakan dalam desain untuk menentukan luas permukaan benda-benda yang berbentuk kerucut, seperti tenda atau topi.
Sejarah rumus luas permukaan kerucut dapat ditelusuri kembali ke zaman Yunani kuno. Matematikawan Yunani, Archimedes, adalah orang pertama yang menemukan rumus ini sekitar tahun 250 SM. Rumus Archimedes untuk luas permukaan kerucut masih digunakan hingga saat ini.
Rumus Luas Permukaan Kerucut
Rumus luas permukaan kerucut merupakan persamaan matematika yang sangat penting dalam berbagai bidang, seperti teknik, arsitektur, dan desain. Rumus ini digunakan untuk menghitung luas permukaan benda-benda yang berbentuk kerucut, seperti tenda, topi, atau corong.
- Pengertian: Persamaan matematika untuk menghitung luas permukaan kerucut.
- Aplikasi: Teknik, arsitektur, dan desain.
- Bentuk: Luas alas (lingkaran) + luas selimut (segitiga).
- Variabel: Jari-jari alas (r), tinggi kerucut (t), dan garis pelukis (s).
- Sejarah: Ditemukan oleh Archimedes sekitar tahun 250 SM.
- Contoh: Menghitung luas permukaan tenda berbentuk kerucut.
- Keterkaitan: Terkait dengan konsep luas permukaan dan geometri kerucut.
Rumus luas permukaan kerucut memiliki beberapa aspek penting, antara lain pengertian, aplikasi, bentuk, variabel, sejarah, contoh, dan keterkaitannya dengan konsep matematika lainnya. Aspek-aspek ini saling berkaitan dan memberikan pemahaman yang komprehensif tentang rumus luas permukaan kerucut.
Pengertian
Pengertian rumus luas permukaan kerucut sebagai persamaan matematika sangat penting karena memberikan dasar untuk menghitung luas permukaan kerucut. Persamaan ini memungkinkan kita untuk menentukan luas permukaan kerucut dengan menggunakan variabel-variabel yang diketahui, seperti jari-jari alas dan tinggi kerucut. Tanpa pengertian yang jelas tentang persamaan matematika ini, akan sulit untuk menghitung luas permukaan kerucut secara akurat.
Aplikasi
Rumus luas permukaan kerucut memiliki keterkaitan yang erat dengan bidang teknik, arsitektur, dan desain. Dalam teknik, rumus ini digunakan untuk menghitung luas permukaan benda-benda berbentuk kerucut, seperti tangki penyimpanan, corong, dan pipa. Dengan mengetahui luas permukaan kerucut, insinyur dapat menentukan jumlah bahan yang dibutuhkan dan merancang struktur yang optimal.
Dalam arsitektur, rumus luas permukaan kerucut digunakan untuk menghitung luas atap berbentuk kerucut, seperti pada menara atau kubah. Arsitek memanfaatkan rumus ini untuk merencanakan dan membangun struktur yang estetis dan fungsional. Selain itu, rumus ini juga digunakan dalam desain untuk menentukan luas permukaan benda-benda yang berbentuk kerucut, seperti tenda, topi, atau layar lampu.
Jadi, rumus luas permukaan kerucut merupakan komponen penting dalam bidang teknik, arsitektur, dan desain. Rumus ini memungkinkan para profesional di bidang tersebut untuk menghitung luas permukaan benda-benda berbentuk kerucut secara akurat, sehingga dapat merancang dan membangun struktur serta benda yang optimal dan efisien.
Bentuk
Bentuk rumus luas permukaan kerucut mencerminkan struktur geometris kerucut, yang terdiri dari alas berbentuk lingkaran dan selimut berbentuk segitiga.
-
Luas Alas
Luas alas kerucut berbentuk lingkaran, yang dihitung menggunakan rumus r. Luas alas mewakili area dasar kerucut.
-
Luas Selimut
Luas selimut kerucut adalah luas permukaan kerucut yang tidak termasuk alasnya. Luas selimut berbentuk segitiga, yang dihitung menggunakan rumus r s, di mana s adalah garis pelukis kerucut.
Dengan menggabungkan luas alas dan luas selimut, kita mendapatkan rumus luas permukaan kerucut, yaitu: L = r + r s.
Variabel
Dalam rumus luas permukaan kerucut, terdapat tiga variabel penting yang saling berkaitan, yaitu jari-jari alas (r), tinggi kerucut (t), dan garis pelukis (s).
-
Jari-Jari Alas (r)
Jari-jari alas kerucut (r) adalah jarak dari pusat alas ke tepi alas. Variabel ini mewakili ukuran alas kerucut dan sangat berpengaruh terhadap luas permukaan kerucut.
-
Tinggi Kerucut (t)
Tinggi kerucut (t) adalah jarak dari puncak kerucut ke alas kerucut. Variabel ini mewakili seberapa tinggi kerucut dan juga memengaruhi luas permukaan kerucut.
-
Garis Pelukis (s)
Garis pelukis (s) adalah jarak dari puncak kerucut ke tepi selimut kerucut. Variabel ini mewakili panjang sisi miring segitiga selimut kerucut dan berperan penting dalam menghitung luas selimut kerucut.
Ketiga variabel ini saling terkait dalam rumus luas permukaan kerucut, yaitu: L = r + r s. Dengan mengetahui nilai dari ketiga variabel ini, kita dapat menghitung luas permukaan kerucut dengan mudah dan akurat.
Sejarah
Penemuan rumus luas permukaan kerucut oleh Archimedes sekitar tahun 250 SM merupakan peristiwa penting dalam sejarah matematika. Rumus tersebut menjadi landasan untuk menghitung luas permukaan kerucut dengan akurat, memungkinkan kemajuan dalam berbagai bidang seperti teknik, arsitektur, dan desain.
Sebelum Archimedes menemukan rumus ini, perhitungan luas permukaan kerucut sangat sulit dan tidak akurat. Akibatnya, pengembangan struktur dan benda yang berbentuk kerucut terhambat. Penemuan Archimedes merevolusi bidang matematika dan teknik, dengan menyediakan metode yang andal untuk menghitung luas permukaan kerucut.
Rumus yang ditemukan oleh Archimedes masih digunakan hingga saat ini. Ini menunjukkan pentingnya penemuan Archimedes dan pengaruhnya yang langgeng pada matematika dan bidang lainnya. Rumus luas permukaan kerucut tetap menjadi alat penting untuk menghitung luas permukaan benda-benda berbentuk kerucut, berkontribusi pada kemajuan ilmu pengetahuan dan teknologi.
Contoh
Hubungan antara rumus luas permukaan kerucut dan contoh penghitungan luas permukaan tenda berbentuk kerucut sangat penting. Rumus luas permukaan kerucut memberikan dasar teoretis untuk menghitung luas permukaan tenda, yang merupakan penerapan praktis dari rumus tersebut.
Dalam konteks ini, contoh penghitungan luas permukaan tenda berbentuk kerucut berfungsi sebagai ilustrasi konkret tentang bagaimana rumus luas permukaan kerucut digunakan dalam situasi dunia nyata. Ini menunjukkan pentingnya rumus sebagai alat untuk memecahkan masalah praktis.
Selain itu, contoh ini juga menyoroti keterkaitan antara matematika dan aplikasi praktisnya. Rumus luas permukaan kerucut, yang awalnya dikembangkan sebagai konsep matematika, menjadi sangat berharga dalam bidang-bidang seperti teknik dan desain, memungkinkan perhitungan akurat luas permukaan benda-benda berbentuk kerucut, seperti tenda.
Keterkaitan
Rumus luas permukaan kerucut tidak berdiri sendiri, melainkan memiliki keterkaitan yang erat dengan konsep luas permukaan dan geometri kerucut secara keseluruhan. Keterkaitan ini sangat penting karena memberikan pemahaman yang lebih mendalam tentang rumus tersebut dan bagaimana rumus tersebut diturunkan.
Konsep luas permukaan mengacu pada pengukuran luas total suatu permukaan, dalam hal ini permukaan kerucut. Rumus luas permukaan kerucut dapat dianggap sebagai aplikasi dari konsep luas permukaan untuk menghitung luas permukaan spesifik kerucut yang diberikan.
Selain itu, rumus luas permukaan kerucut juga terkait erat dengan geometri kerucut. Geometri kerucut mempelajari sifat dan hubungan bentuk kerucut, termasuk luas permukaannya. Rumus luas permukaan kerucut diturunkan berdasarkan prinsip-prinsip geometri kerucut, seperti teorema Pythagoras dan sifat-sifat segitiga dan lingkaran.
Jadi, keterkaitan rumus luas permukaan kerucut dengan konsep luas permukaan dan geometri kerucut sangat penting untuk memahami rumus tersebut secara komprehensif. Keterkaitan ini memberikan dasar teoretis dan kontekstual untuk rumus tersebut, menjadikannya alat yang ampuh untuk menghitung luas permukaan kerucut dalam berbagai aplikasi praktis.
Pertanyaan Umum tentang Rumus Luas Permukaan Kerucut
Berikut adalah beberapa pertanyaan umum tentang rumus luas permukaan kerucut, beserta jawabannya:
Pertanyaan 1: Apa yang dimaksud dengan rumus luas permukaan kerucut?
Jawaban: Rumus luas permukaan kerucut adalah persamaan matematika yang digunakan untuk menentukan luas permukaan kerucut, yang terdiri dari luas alas berbentuk lingkaran dan luas selimut berbentuk segitiga.
Pertanyaan 2: Kapan dan oleh siapa rumus luas permukaan kerucut ditemukan?
Jawaban: Rumus luas permukaan kerucut ditemukan oleh Archimedes sekitar tahun 250 SM.
Pertanyaan 3: Apa saja variabel yang terlibat dalam rumus luas permukaan kerucut?
Jawaban: Variabel yang terlibat dalam rumus luas permukaan kerucut adalah jari-jari alas (r), tinggi kerucut (t), dan garis pelukis (s).
Pertanyaan 4: Apa kaitan antara rumus luas permukaan kerucut dan geometri kerucut?
Jawaban: Rumus luas permukaan kerucut diturunkan berdasarkan prinsip-prinsip geometri kerucut, seperti teorema Pythagoras dan sifat-sifat segitiga dan lingkaran.
Kesimpulannya, rumus luas permukaan kerucut merupakan alat penting untuk menghitung luas permukaan benda-benda berbentuk kerucut. Rumus ini memiliki sejarah yang panjang dan keterkaitan erat dengan geometri kerucut. Memahami rumus luas permukaan kerucut sangat penting dalam berbagai bidang, seperti teknik, arsitektur, dan desain.
Transisi ke bagian selanjutnya:
Tips dalam menghitung luas permukaan kerucut
Berikut adalah beberapa tips untuk membantu Anda dalam menghitung luas permukaan kerucut:
Tip 1: Pahami rumus luas permukaan kerucut
Pahami rumus L = r + rs, di mana r adalah jari-jari alas kerucut dan s adalah garis pelukis kerucut.
Tip 2: Identifikasi variabel yang diketahui
Sebelum menggunakan rumus, pastikan Anda telah mengidentifikasi nilai jari-jari alas (r) dan tinggi kerucut (t). Garis pelukis (s) dapat dihitung menggunakan rumus s = (r + t).
Tip 3: Gunakan kalkulator yang tepat
Gunakan kalkulator ilmiah atau kalkulator daring yang dapat menghitung nilai dan akar kuadrat dengan akurat.
Tip 4: Periksa kembali satuan
Pastikan Anda menggunakan satuan yang konsisten saat mengganti variabel ke dalam rumus. Misalnya, jika r dan t dalam sentimeter, maka luas permukaan yang dihasilkan juga akan dalam sentimeter persegi.
Tip 5: Berlatih soal
Berlatihlah mengerjakan soal-soal luas permukaan kerucut untuk meningkatkan pemahaman dan keterampilan Anda.
Dengan mengikuti tips ini, Anda dapat menghitung luas permukaan kerucut secara akurat dan efisien.
Kesimpulan:
Youtube Video:










