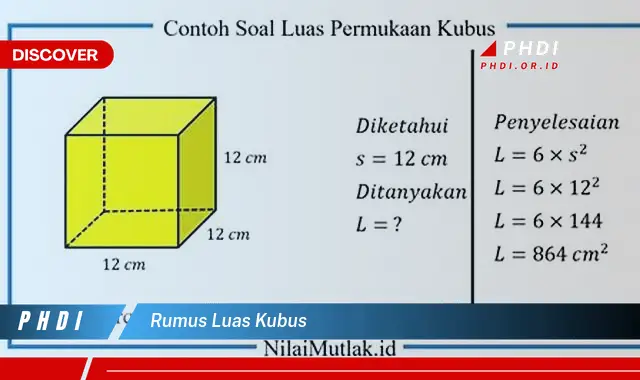
Rumus luas kubus adalah rumus yang digunakan untuk menghitung luas permukaan kubus. Rumus ini menyatakan bahwa luas permukaan kubus adalah 6 kali luas salah satu sisinya. Jadi, jika panjang sisi kubus adalah s, maka luas permukaan kubus adalah 6s. Rumus ini dapat digunakan untuk menghitung luas permukaan kubus dengan berbagai ukuran.
Rumus luas kubus sangat penting dalam berbagai bidang, seperti matematika, fisika, dan teknik. Dalam matematika, rumus ini digunakan untuk menghitung luas permukaan dan volume kubus. Dalam fisika, rumus ini digunakan untuk menghitung gaya yang bekerja pada permukaan kubus. Dalam teknik, rumus ini digunakan untuk menghitung luas permukaan benda-benda yang berbentuk kubus.
Rumus luas kubus pertama kali ditemukan oleh matematikawan Yunani kuno, Euclid. Rumus ini pertama kali diterbitkan dalam buku Euclid yang berjudul “Elements”. Sejak saat itu, rumus ini telah digunakan secara luas dalam berbagai bidang.
Rumus Luas Kubus
Rumus luas kubus merupakan konsep dasar dalam geometri yang memiliki berbagai aspek penting:
- Definisi: Rumus yang menghitung luas permukaan kubus.
- Rumus: L = 6 s, dengan s adalah panjang sisi kubus.
- Satuan: Luas permukaan dalam satuan luas, seperti cm atau m.
- Aplikasi: Menghitung luas permukaan benda berbentuk kubus.
- Sejarah: Ditemukan oleh Euclid pada zaman Yunani kuno.
- Keterkaitan: Berhubungan dengan konsep volume kubus (V = s).
- Contoh: Kubus dengan sisi 5 cm memiliki luas permukaan 150 cm.
Pemahaman tentang aspek-aspek ini sangat penting untuk menguasai konsep rumus luas kubus. Aspek-aspek ini saling terkait dan memberikan pemahaman yang komprehensif tentang cara menghitung dan menerapkan rumus ini dalam berbagai konteks.
Definisi
Definisi rumus luas kubus sangat penting karena memberikan dasar pemahaman tentang konsep tersebut. Definisi ini menetapkan bahwa rumus ini digunakan untuk menghitung luas permukaan kubus, suatu bangun ruang tiga dimensi yang memiliki enam sisi berbentuk persegi yang sama. Definisi ini mengklarifikasi tujuan dan fungsi rumus, menjadikannya landasan bagi eksplorasi lebih lanjut tentang rumus luas kubus.
Rumus
Rumus L = 6 s merupakan komponen penting dari rumus luas kubus. Rumus ini menunjukkan hubungan antara panjang sisi kubus (s) dan luas permukaannya (L). Menurut rumus ini, luas permukaan kubus adalah enam kali luas salah satu sisinya. Komponen ini sangat penting karena memungkinkan kita untuk menghitung luas permukaan kubus dengan mudah dan akurat, hanya dengan mengetahui panjang sisinya.
Satuan
Satuan luas permukaan merupakan komponen penting dalam rumus luas kubus karena menunjukkan hasil pengukuran luas permukaan. Satuan seperti cm (sentimeter persegi) dan m (meter persegi) memberikan konteks dan makna pada nilai luas permukaan yang dihitung menggunakan rumus. Tanpa satuan yang tepat, hasil perhitungan akan menjadi tidak berarti dan sulit untuk ditafsirkan.
Aplikasi
Aplikasi rumus luas kubus sangatlah luas, terutama dalam menghitung luas permukaan benda-benda berbentuk kubus. Rumus ini memiliki peran penting dalam berbagai bidang, seperti arsitektur, desain, dan pengemasan.
-
Arsitektur
Dalam arsitektur, rumus luas kubus digunakan untuk menghitung luas permukaan bangunan atau ruangan yang berbentuk kubus. Hal ini penting untuk menentukan kebutuhan material, seperti cat atau wallpaper, serta untuk memperkirakan biaya pembangunan.
-
Desain
Dalam desain, rumus luas kubus digunakan untuk menghitung luas permukaan benda-benda berbentuk kubus, seperti kotak, kemasan, atau furnitur. Hal ini penting untuk memastikan bahwa benda tersebut memiliki ukuran dan tampilan yang sesuai dengan kebutuhan dan estetika yang diinginkan.
-
Pengemasan
Dalam pengemasan, rumus luas kubus digunakan untuk menghitung luas permukaan kemasan berbentuk kubus. Hal ini penting untuk menentukan jumlah bahan kemasan yang dibutuhkan, serta untuk mengoptimalkan ruang penyimpanan dan transportasi.
Dengan demikian, rumus luas kubus memiliki aplikasi yang sangat luas dan penting dalam berbagai bidang, terutama dalam menghitung luas permukaan benda-benda berbentuk kubus.
Sejarah
Penemuan rumus luas kubus oleh Euclid pada zaman Yunani kuno merupakan tonggak penting dalam perkembangan matematika. Rumus ini telah menjadi dasar bagi konsep geometri dan pengukuran selama berabad-abad.
-
Peran Penting dalam Geometri
Rumus luas kubus memberikan dasar teoritis untuk menghitung luas permukaan kubus, bangun ruang tiga dimensi yang umum ditemukan dalam kehidupan sehari-hari. Rumus ini menjadi landasan bagi pengembangan konsep luas permukaan dan volume bangun ruang lainnya.
-
Pengaruh pada Arsitektur dan Teknik
Rumus luas kubus memiliki pengaruh besar pada bidang arsitektur dan teknik. Arsitek dan insinyur menggunakan rumus ini untuk menghitung luas permukaan bangunan dan struktur yang berbentuk kubus atau memiliki elemen kubus. Hal ini penting untuk perencanaan dan konstruksi yang akurat.
-
Aplikasi dalam Ilmu Pengetahuan dan Teknologi
Rumus luas kubus juga diterapkan dalam berbagai bidang ilmu pengetahuan dan teknologi. Misalnya, dalam fisika, rumus ini digunakan untuk menghitung luas permukaan partikel kubik, dan dalam kimia, digunakan untuk menghitung luas permukaan kristal.
-
Warisan Matematika
Penemuan rumus luas kubus oleh Euclid merupakan bukti kecerdasan dan kontribusi matematikawan Yunani kuno terhadap perkembangan matematika. Rumus ini terus digunakan hingga saat ini, menunjukkan warisan matematika yang abadi.
Dengan demikian, sejarah penemuan rumus luas kubus oleh Euclid pada zaman Yunani kuno memiliki implikasi mendalam pada perkembangan matematika, arsitektur, teknik, ilmu pengetahuan, dan teknologi.
Keterkaitan
Rumus luas kubus memiliki keterkaitan yang erat dengan konsep volume kubus. Volume kubus dihitung menggunakan rumus V = s, dengan s adalah panjang sisi kubus. Keterkaitan ini memberikan pemahaman yang lebih komprehensif tentang sifat-sifat kubus dan hubungan antara luas permukaan dan volumenya.
-
Perhitungan Volume Kubus
Rumus volume kubus (V = s) memungkinkan kita untuk menentukan volume kubus jika kita mengetahui panjang sisinya. Hal ini penting dalam berbagai aplikasi, seperti menghitung kapasitas wadah berbentuk kubus atau menentukan volume suatu benda yang berbentuk kubus.
-
Rasio Luas Permukaan dan Volume
Keterkaitan antara luas permukaan dan volume kubus memberikan wawasan tentang hubungan geometrik bangun ruang ini. Rasio luas permukaan terhadap volume kubus berbanding terbalik dengan panjang sisinya. Artinya, semakin kecil panjang sisi kubus, semakin besar rasio luas permukaan terhadap volumenya.
-
Aplikasi dalam Fisika dan Kimia
Keterkaitan antara luas permukaan dan volume kubus memiliki aplikasi yang luas dalam bidang fisika dan kimia. Dalam fisika, hal ini digunakan untuk menghitung laju perpindahan panas dan gaya yang bekerja pada permukaan kubus. Dalam kimia, hal ini digunakan untuk menentukan luas permukaan partikel zat padat.
-
Pemahaman Komprehensif tentang Kubus
Memahami keterkaitan antara rumus luas kubus dan volume kubus memberikan pemahaman yang komprehensif tentang sifat-sifat kubus. Hal ini memungkinkan kita untuk menganalisis dan menyelesaikan masalah yang melibatkan kubus dengan lebih efektif.
Dengan demikian, keterkaitan antara rumus luas kubus dan konsep volume kubus sangat penting untuk memahami sifat-sifat kubus secara menyeluruh dan menerapkannya dalam berbagai aplikasi di berbagai bidang.
Contoh
Contoh yang diberikan menunjukkan aplikasi langsung dari rumus luas kubus dalam menghitung luas permukaan kubus. Contoh tersebut menyajikan kubus dengan panjang sisi 5 cm dan menghitung luas permukaannya menjadi 150 cm.
-
Penggunaan Rumus
Contoh ini menunjukkan bagaimana rumus luas kubus (L = 6 s) diterapkan untuk menghitung luas permukaan kubus. Dengan mensubstitusikan panjang sisi (s = 5 cm) ke dalam rumus, kita mendapatkan luas permukaan (L = 150 cm).
-
Interpretasi Hasil
Hasil perhitungan (150 cm) menunjukkan luas permukaan total kubus, yang merupakan jumlah luas keenam sisinya. Hasil ini penting untuk berbagai aplikasi, seperti menentukan jumlah bahan yang dibutuhkan untuk menutupi permukaan kubus atau menghitung gaya yang bekerja pada permukaannya.
-
Penerapan dalam Kehidupan Nyata
Contoh ini dapat diterapkan dalam berbagai situasi kehidupan nyata, seperti menghitung luas permukaan kotak kado, kubus es, atau wadah penyimpanan berbentuk kubus. Memahami rumus luas kubus memungkinkan kita menyelesaikan masalah ini dengan cepat dan akurat.
Dengan demikian, contoh yang diberikan tidak hanya mengilustrasikan penggunaan rumus luas kubus tetapi juga menyoroti penerapannya dalam konteks kehidupan nyata. Contoh ini memperkuat pemahaman tentang rumus dan relevansinya dalam berbagai bidang.
Pertanyaan Umum tentang Rumus Luas Kubus
Berikut adalah beberapa pertanyaan umum yang sering diajukan tentang rumus luas kubus:
Pertanyaan 1: Bagaimana cara menggunakan rumus luas kubus?
Rumus luas kubus adalah L = 6 s, dengan L adalah luas permukaan kubus dan s adalah panjang sisi kubus. Untuk menggunakan rumus ini, Anda hanya perlu mengganti nilai panjang sisi kubus ke dalam rumus dan menghitung hasilnya.
Pertanyaan 2: Satuan apa yang digunakan untuk menyatakan luas permukaan kubus?
Luas permukaan kubus dinyatakan dalam satuan luas, seperti sentimeter persegi (cm) atau meter persegi (m).
Pertanyaan 3: Mengapa penting untuk mengetahui rumus luas kubus?
Rumus luas kubus penting karena memungkinkan kita menghitung luas permukaan kubus dengan mudah dan akurat. Hal ini berguna dalam berbagai aplikasi, seperti arsitektur, desain, dan pengemasan.
Pertanyaan 4: Siapa yang menemukan rumus luas kubus?
Rumus luas kubus pertama kali ditemukan oleh matematikawan Yunani kuno, Euclid.
Dengan memahami rumus luas kubus dan penerapannya, kita dapat menyelesaikan masalah yang melibatkan kubus dengan lebih efektif dan akurat.
Selain pertanyaan umum di atas, masih banyak pertanyaan lain yang dapat diajukan mengenai rumus luas kubus. Untuk informasi lebih lanjut, Anda dapat berkonsultasi dengan sumber terpercaya atau berkonsultasi dengan ahli di bidang matematika atau geometri.
Tips Menghitung Luas Permukaan Kubus
Berikut adalah beberapa tips yang dapat membantu Anda menghitung luas permukaan kubus dengan mudah dan akurat:
Tip 1: Pahami konsep kubusSebelum menghitung luas permukaan kubus, penting untuk memahami konsep kubus itu sendiri. Kubus adalah bangun ruang tiga dimensi yang memiliki enam sisi berbentuk persegi yang sama ukurannya.Tip 2: Identifikasi panjang sisi kubusUntuk menghitung luas permukaan kubus, Anda perlu mengetahui panjang salah satu sisinya. Panjang sisi kubus biasanya dilambangkan dengan huruf “s”.Tip 3: Gunakan rumus luas permukaan kubusRumus untuk menghitung luas permukaan kubus adalah L = 6 s, dengan L adalah luas permukaan dan s adalah panjang sisi kubus.Tip 4: Substitusikan panjang sisi ke dalam rumusSetelah Anda mengetahui panjang sisi kubus, substitusikan nilai tersebut ke dalam rumus luas permukaan kubus. Misalnya, jika panjang sisi kubus adalah 5 cm, maka luas permukaannya adalah L = 6 * 5^2 = 150 cm.Tip 5: Gunakan satuan yang sesuaiLuas permukaan kubus dinyatakan dalam satuan luas, seperti sentimeter persegi (cm) atau meter persegi (m). Pastikan untuk menggunakan satuan yang sesuai dalam perhitungan Anda.Dengan mengikuti tips ini, Anda dapat menghitung luas permukaan kubus dengan cepat dan akurat. Pemahaman yang baik tentang konsep kubus dan penerapan rumus luas permukaan kubus sangat penting untuk menyelesaikan masalah yang melibatkan bangun ruang ini.
Kesimpulan
Rumus luas permukaan kubus adalah alat penting untuk menghitung luas permukaan bangun ruang tiga dimensi ini. Dengan memahami konsep kubus, mengidentifikasi panjang sisinya, dan menggunakan rumus yang benar, Anda dapat menghitung luas permukaan kubus dengan mudah dan akurat. Tips yang diuraikan dalam artikel ini akan membantu Anda menguasai konsep ini dan menerapkannya dalam berbagai situasi.
Youtube Video:










