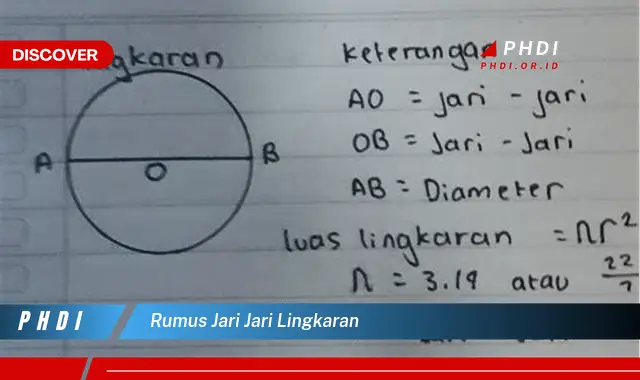
Rumus jari-jari lingkaran adalah sebuah persamaan yang digunakan untuk menghitung jari-jari lingkaran. Persamaan ini menggunakan nilai phi () yang merupakan konstanta matematika sekitar 3,14. Rumus jari-jari lingkaran dapat dituliskan sebagai:
r = d / 2
di mana:
- r adalah jari-jari lingkaran
- d adalah diameter lingkaran
- adalah konstanta matematika sekitar 3,14
Rumus ini penting karena memungkinkan kita untuk menghitung jari-jari lingkaran ketika kita mengetahui diameternya. Ini berguna dalam berbagai aplikasi, seperti teknik, desain, dan fisika. Misalnya, rumus ini dapat digunakan untuk menghitung jari-jari roda, menentukan ukuran lubang, atau menghitung luas dan keliling lingkaran.
Rumus jari-jari lingkaran pertama kali ditemukan oleh matematikawan Yunani Archimedes sekitar tahun 250 SM. Sejak itu, rumus ini telah digunakan oleh para ilmuwan dan insinyur selama berabad-abad.
Rumus Jari-jari Lingkaran
Rumus jari-jari lingkaran sangat penting dalam berbagai bidang, seperti teknik, desain, dan fisika. Rumus ini memiliki beberapa aspek penting, yaitu:
- Definisi: Persamaan untuk mencari jari-jari lingkaran, menggunakan diameter dan phi ().
- Aplikasi: Digunakan untuk menghitung jari-jari roda, menentukan ukuran lubang, menghitung luas dan keliling lingkaran.
- Sejarah: Pertama kali ditemukan oleh Archimedes pada 250 SM.
- Konstanta: Menggunakan phi (), sebuah konstanta matematika sekitar 3,14.
- Satuan: Jari-jari lingkaran dinyatakan dalam satuan panjang, seperti meter atau sentimeter.
- Turunan: Dapat digunakan untuk menurunkan rumus luas dan keliling lingkaran.
- Pembuktian: Dapat dibuktikan menggunakan geometri dasar.
Rumus jari-jari lingkaran sangat penting karena memungkinkan kita untuk menghitung jari-jari lingkaran dengan mudah dan akurat. Rumus ini memiliki sejarah panjang dan telah digunakan oleh para ilmuwan dan insinyur selama berabad-abad. Memahami aspek-aspek penting dari rumus ini sangat penting untuk menggunakannya secara efektif dalam berbagai aplikasi.
Definisi
Definisi rumus jari-jari lingkaran sangat penting karena memberikan dasar teoretis untuk menghitung jari-jari lingkaran. Persamaan ini menggunakan diameter lingkaran dan konstanta matematika phi () untuk menentukan jari-jarinya.
-
Komponen Persamaan
Persamaan rumus jari-jari lingkaran terdiri dari tiga komponen utama: jari-jari (r), diameter (d), dan phi (). Jari-jari adalah besaran yang ingin kita cari, diameter adalah jarak melintasi lingkaran melalui titik pusatnya, dan phi adalah konstanta matematika sekitar 3,14.
-
Penerapan dalam Kehidupan Nyata
Rumus jari-jari lingkaran memiliki banyak penerapan dalam kehidupan nyata, seperti menghitung jari-jari roda, menentukan ukuran lubang, atau menghitung luas dan keliling lingkaran. Misalnya, dalam teknik, rumus ini digunakan untuk merancang roda gigi dan poros, sementara dalam arsitektur, rumus ini digunakan untuk menghitung dimensi kubah dan lengkungan.
-
Implikasi untuk Rumus Jari-jari Lingkaran
Definisi rumus jari-jari lingkaran menjadi dasar untuk menurunkan rumus luas dan keliling lingkaran. Dengan mengetahui jari-jari lingkaran, kita dapat dengan mudah menghitung luas dan kelilingnya menggunakan rumus yang sesuai.
Dengan memahami definisi rumus jari-jari lingkaran, kita dapat menggunakannya secara efektif untuk menghitung jari-jari lingkaran dengan akurat dan efisien. Definisi ini memberikan landasan yang kokoh untuk penerapan rumus ini dalam berbagai bidang, mulai dari teknik hingga fisika.
Aplikasi
Rumus jari-jari lingkaran memiliki berbagai aplikasi dalam kehidupan nyata, yang menjadikannya alat yang penting dalam berbagai bidang. Beberapa aplikasi utama meliputi:
-
Menghitung Jari-jari Roda
Rumus jari-jari lingkaran sangat penting dalam teknik, khususnya dalam desain roda. Dengan mengetahui diameter roda, insinyur dapat menghitung jari-jarinya menggunakan rumus ini. Ini memastikan bahwa roda memiliki ukuran dan bentuk yang tepat untuk aplikasi yang dimaksudkan.
-
Menentukan Ukuran Lubang
Dalam konstruksi dan manufaktur, rumus jari-jari lingkaran digunakan untuk menentukan ukuran lubang. Dengan mengetahui diameter lubang yang diinginkan, pekerja dapat menghitung jari-jarinya menggunakan rumus ini. Hal ini memastikan bahwa lubang memiliki ukuran yang tepat untuk menampung komponen atau struktur lain.
-
Menghitung Luas dan Keliling Lingkaran
Rumus jari-jari lingkaran juga digunakan untuk menghitung luas dan keliling lingkaran. Dengan mengetahui jari-jari lingkaran, kita dapat menggunakan rumus yang sesuai untuk menghitung luas dan kelilingnya. Ini berguna dalam berbagai aplikasi, seperti menghitung luas permukaan objek berbentuk lingkaran atau menentukan panjang pagar yang mengelilingi sebuah taman berbentuk lingkaran.
Berbagai aplikasi ini menunjukkan pentingnya rumus jari-jari lingkaran dalam kehidupan nyata. Rumus ini merupakan alat serbaguna yang memungkinkan kita untuk memecahkan masalah dan merancang solusi di berbagai bidang, mulai dari teknik hingga fisika.
Sejarah
Sejarah penemuan rumus jari-jari lingkaran oleh Archimedes pada 250 SM memainkan peran penting dalam perkembangan rumus tersebut. Archimedes, seorang matematikawan Yunani kuno, dianggap sebagai salah satu matematikawan terbesar sepanjang masa. Penemuannya tentang rumus jari-jari lingkaran merupakan tonggak sejarah dalam geometri.
Sebelum Archimedes, tidak ada rumus umum untuk menghitung jari-jari lingkaran. Akibatnya, perhitungan jari-jari lingkaran dilakukan dengan metode yang kurang akurat dan efisien. Penemuan Archimedes memberikan solusi yang elegan dan universal untuk masalah ini.
Rumus jari-jari lingkaran yang ditemukan Archimedes didasarkan pada prinsip-prinsip geometri dasar. Dia membuktikan bahwa jari-jari lingkaran sama dengan setengah diameternya, yang dapat dihitung menggunakan pengukuran sederhana. Penemuan ini merevolusi cara orang menghitung jari-jari lingkaran, menjadikannya lebih mudah dan akurat.
Penemuan Archimedes tentang rumus jari-jari lingkaran memiliki dampak yang signifikan terhadap berbagai bidang, termasuk matematika, fisika, dan teknik. Rumus ini menjadi dasar untuk menghitung luas dan keliling lingkaran, serta untuk memecahkan berbagai masalah geometri lainnya. Tanpa penemuan Archimedes, kemajuan dalam bidang-bidang ini akan jauh lebih lambat dan sulit.
Konstanta
Konstanta $\pi$ memegang peranan penting dalam rumus jari-jari lingkaran, yang menjadikannya alat yang ampuh untuk menghitung jari-jari lingkaran secara akurat. Berikut adalah beberapa aspek penting dari hubungan antara $\pi$ dan rumus jari-jari lingkaran:
-
Definisi dan Peran $\pi$
$\pi$ adalah konstanta matematika yang mewakili rasio lingkaran keliling lingkaran dengan diameternya. Ini adalah nilai irasional yang kira-kira sama dengan 3,14. Dalam rumus jari-jari lingkaran, $\pi$ digunakan untuk memastikan bahwa jari-jari dihitung secara akurat, terlepas dari ukuran atau bentuk lingkaran.
-
Aplikasi dalam Kehidupan Nyata
Penggunaan $\pi$ dalam rumus jari-jari lingkaran memiliki berbagai aplikasi dalam kehidupan nyata, seperti menghitung jari-jari roda, menentukan ukuran lubang, dan menghitung luas dan keliling lingkaran. Misalnya, dalam teknik, $\pi$ digunakan untuk merancang roda gigi dan poros, sementara dalam arsitektur, $\pi$ digunakan untuk menghitung dimensi kubah dan lengkungan.
-
Implikasi untuk Rumus Jari-jari Lingkaran
Keberadaan $\pi$ dalam rumus jari-jari lingkaran memungkinkan kita untuk menghitung jari-jari lingkaran dengan tingkat presisi yang tinggi. Tanpa $\pi$, rumus jari-jari lingkaran tidak akan akurat dan dapat menyebabkan kesalahan dalam perhitungan.
Dengan memahami hubungan antara $\pi$ dan rumus jari-jari lingkaran, kita dapat menggunakannya secara efektif untuk menghitung jari-jari lingkaran dengan akurat dan efisien. Konstanta $\pi$ adalah komponen penting dari rumus ini, yang menjadikannya alat yang berharga dalam berbagai bidang, mulai dari teknik hingga fisika.
Satuan
Satuan jari-jari lingkaran merupakan komponen penting dalam rumus jari-jari lingkaran karena memastikan hasil perhitungan akurat dan dapat diandalkan. Jari-jari lingkaran harus dinyatakan dalam satuan panjang yang sesuai, seperti meter atau sentimeter, untuk memastikan bahwa hasil perhitungan juga dinyatakan dalam satuan panjang yang tepat.
Penggunaan satuan panjang yang tepat sangat penting karena rumus jari-jari lingkaran melibatkan perhitungan matematis. Jika jari-jari lingkaran dinyatakan dalam satuan yang berbeda, seperti inci atau kaki, maka hasil perhitungan akan salah dan tidak dapat digunakan.
Oleh karena itu, satuan jari-jari lingkaran harus selalu dinyatakan dalam satuan panjang yang konsisten untuk memastikan akurasi dan keandalan hasil perhitungan.
Turunan
Turunan dari rumus jari-jari lingkaran memiliki peran penting dalam memperluas kegunaannya. Dengan mengetahui jari-jari lingkaran, kita dapat menurunkan rumus untuk menghitung luas dan keliling lingkaran.
Rumus luas lingkaran diturunkan dengan menggunakan rumus jari-jari lingkaran dan mengalikannya dengan dirinya sendiri, karena luas lingkaran sebanding dengan kuadrat jari-jarinya. Demikian pula, rumus keliling lingkaran diturunkan dengan menggunakan rumus jari-jari lingkaran dan mengalikannya dengan 2, karena keliling lingkaran sebanding dengan kelilingnya.
Dengan demikian, turunan dari rumus jari-jari lingkaran memungkinkan kita untuk memperoleh rumus luas dan keliling lingkaran, yang merupakan besaran penting dalam berbagai bidang, seperti matematika, fisika, dan teknik.
Pembuktian
Pembuktian rumus jari-jari lingkaran menggunakan geometri dasar memiliki peran penting dalam membangun dasar teoretis yang kokoh untuk rumus tersebut. Pembuktian ini memberikan pemahaman yang jelas tentang bagaimana rumus tersebut diturunkan dan mengapa rumus tersebut berlaku.
-
Landasan Geometris
Pembuktian rumus jari-jari lingkaran didasarkan pada prinsip-prinsip geometri dasar, seperti Teorema Pythagoras dan sifat-sifat lingkaran. Dengan menggunakan prinsip-prinsip ini, dapat ditunjukkan bahwa jari-jari lingkaran sama dengan setengah diameternya.
-
Konstruksi Geometris
Pembuktian ini melibatkan konstruksi geometris, seperti menggambar lingkaran dan membagi diameternya menjadi dua bagian yang sama. Konstruksi ini membantu memvisualisasikan hubungan antara jari-jari dan diameter, sehingga memudahkan untuk memahami pembuktian.
-
Implikasi untuk Rumus
Pembuktian menggunakan geometri dasar memberikan dasar yang kuat untuk rumus jari-jari lingkaran. Pembuktian ini menunjukkan bahwa rumus tersebut benar secara matematis dan dapat digunakan dengan percaya diri untuk menghitung jari-jari lingkaran.
Dengan memahami pembuktian rumus jari-jari lingkaran menggunakan geometri dasar, kita dapat lebih menghargai ketelitian dan keabsahan rumus tersebut. Pembuktian ini memberikan landasan yang kokoh untuk aplikasi rumus ini dalam berbagai bidang, seperti teknik, fisika, dan matematika.
Tanya Jawab Umum tentang Rumus Jari-jari Lingkaran
Rumus jari-jari lingkaran merupakan konsep penting yang banyak digunakan dalam berbagai bidang. Untuk memberikan pemahaman yang lebih baik, berikut beberapa tanya jawab umum yang sering diajukan:
Pertanyaan 1: Apa itu rumus jari-jari lingkaran?
Rumus jari-jari lingkaran adalah persamaan matematika yang digunakan untuk mencari jari-jari lingkaran. Rumus ini menggunakan nilai phi () dan diameter lingkaran.
Pertanyaan 2: Bagaimana cara menggunakan rumus jari-jari lingkaran?
Untuk menggunakan rumus jari-jari lingkaran, Anda perlu mengetahui diameter lingkaran. Setelah itu, Anda dapat memasukkan nilai diameter ke dalam rumus dan menghitung jari-jarinya.
Pertanyaan 3: Apa saja aplikasi rumus jari-jari lingkaran?
Rumus jari-jari lingkaran memiliki banyak aplikasi dalam kehidupan nyata, seperti menghitung jari-jari roda, menentukan ukuran lubang, atau menghitung luas dan keliling lingkaran.
Pertanyaan 4: Mengapa rumus jari-jari lingkaran penting?
Rumus jari-jari lingkaran penting karena memungkinkan kita untuk menentukan jari-jari lingkaran dengan mudah dan akurat. Rumus ini memiliki sejarah panjang dan telah banyak digunakan dalam berbagai bidang.
Dengan memahami rumus jari-jari lingkaran dan aplikasinya, kita dapat menggunakannya secara efektif untuk memecahkan masalah dan merancang solusi di berbagai bidang.
Catatan: Silakan merujuk ke sumber terpercaya untuk informasi lebih lanjut tentang rumus jari-jari lingkaran dan aplikasinya.
Tips Menggunakan Rumus Jari-jari Lingkaran
Rumus jari-jari lingkaran merupakan alat penting yang digunakan dalam berbagai bidang. Berikut adalah beberapa tips untuk menggunakan rumus ini secara efektif:
Tip 1: Pahami Konsep Dasar
Sebelum menggunakan rumus jari-jari lingkaran, penting untuk memahami konsep dasar yang terlibat. Ini termasuk mengetahui apa itu jari-jari, diameter, dan konstanta pi ().
Tip 2: Gunakan Satuan yang Konsisten
Saat menggunakan rumus jari-jari lingkaran, pastikan untuk menggunakan satuan yang konsisten untuk jari-jari dan diameter. Misalnya, jika jari-jari diberikan dalam sentimeter, maka diameter juga harus dalam sentimeter.
Tip 3: Periksa Hasil Anda
Setelah menghitung jari-jari lingkaran, sebaiknya periksa kembali hasil Anda. Ini dapat dilakukan dengan membandingkan hasilnya dengan pengukuran aktual atau dengan menggunakan metode alternatif untuk menghitung jari-jari.
Tip 4: Terapkan dalam Praktik
Rumus jari-jari lingkaran memiliki banyak aplikasi praktis. Luangkan waktu untuk mengeksplorasi aplikasi ini dan mencoba menerapkan rumus dalam situasi yang berbeda.
Tip 5: Cari Sumber yang Andal
Jika Anda membutuhkan informasi lebih lanjut atau memiliki pertanyaan tentang rumus jari-jari lingkaran, cari sumber yang andal, seperti buku teks atau artikel jurnal.
Dengan mengikuti tips ini, Anda dapat menggunakan rumus jari-jari lingkaran secara efektif dan akurat dalam berbagai aplikasi.
Kesimpulan
Rumus jari-jari lingkaran adalah alat yang ampuh yang dapat digunakan untuk memecahkan berbagai masalah dalam matematika, fisika, dan teknik. Dengan memahami konsep dasar, menggunakan satuan yang konsisten, memeriksa hasil, menerapkan dalam praktik, dan mencari sumber yang andal, Anda dapat memaksimalkan penggunaan rumus ini dan memperoleh pemahaman yang lebih baik tentang geometri lingkaran.
Youtube Video:










