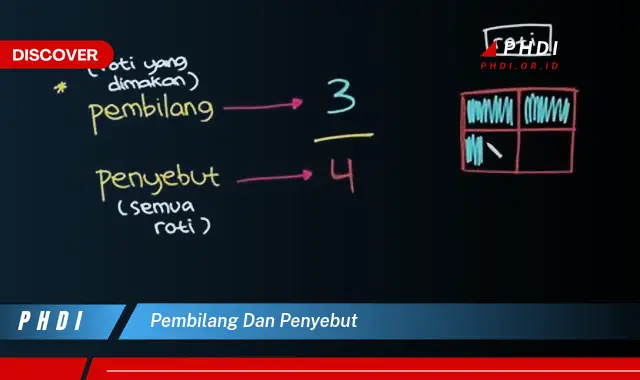
Pembilang dan penyebut adalah dua istilah yang digunakan dalam matematika untuk menyebut bagian dari pecahan. Pembilang adalah angka yang terletak di atas garis pemisah, sedangkan penyebut adalah angka yang terletak di bawah garis pemisah. Misalnya, dalam pecahan 1/2, 1 adalah pembilang dan 2 adalah penyebut.
Pembilang dan penyebut sangat penting dalam matematika. Mereka digunakan untuk menunjukkan nilai pecahan, membandingkan pecahan, dan melakukan operasi matematika pada pecahan. Misalnya, untuk membandingkan dua pecahan, kita dapat melihat pembilang dan penyebutnya. Pecahan dengan pembilang lebih besar dari penyebutnya lebih besar dari 1, sedangkan pecahan dengan pembilang lebih kecil dari penyebutnya lebih kecil dari 1.
Konsep pembilang dan penyebut telah digunakan selama berabad-abad. Mereka pertama kali digunakan oleh orang Babilonia sekitar 4000 tahun yang lalu. Sejak saat itu, pembilang dan penyebut telah menjadi bagian penting dari matematika dan terus digunakan hingga saat ini.
Pembilang dan Penyebut
Pembilang dan penyebut merupakan dua aspek penting dalam matematika, khususnya dalam memahami pecahan. Berikut adalah tujuh aspek penting terkait pembilang dan penyebut:
- Letak: Pembilang di atas garis, penyebut di bawah garis
- Fungsi: Menunjukkan nilai pecahan
- Perbandingan: Membandingkan nilai pecahan
- Operasi: Melakukan operasi matematika pada pecahan
- Sejarah: Digunakan sejak zaman Babilonia
- Jenis: Pecahan biasa, desimal, persen
- Aplikasi: Berbagai bidang, seperti sains, teknik, dan keuangan
Secara keseluruhan, pembilang dan penyebut memainkan peran penting dalam matematika. Mereka memungkinkan kita untuk menyatakan, membandingkan, dan memanipulasi pecahan, yang merupakan konsep dasar dalam matematika dan memiliki aplikasi yang luas dalam kehidupan sehari-hari.
Letak
Letak pembilang di atas garis dan penyebut di bawah garis merupakan aspek penting dari pecahan. Penempatan ini secara jelas menunjukkan hubungan antara kedua bilangan dan nilai pecahan yang diwakilinya.
-
Membedakan Pembilang dan Penyebut
Letak pembilang di atas garis dan penyebut di bawah garis membantu membedakan kedua bilangan dengan jelas. Hal ini penting untuk menghindari kebingungan dan memastikan pemahaman yang benar tentang pecahan. -
Menunjukkan Hubungan
Penempatan pembilang dan penyebut juga menunjukkan hubungan antara kedua bilangan. Pembilang menunjukkan jumlah bagian yang diambil dari keseluruhan, sedangkan penyebut menunjukkan jumlah bagian yang sama dalam keseluruhan. Letaknya yang berlawanan membantu memvisualisasikan hubungan ini. -
Menentukan Nilai Pecahan
Letak pembilang dan penyebut sangat penting dalam menentukan nilai pecahan. Nilai pecahan dihitung dengan membagi pembilang dengan penyebut. Penempatan yang tepat memastikan perhitungan yang akurat. -
Konsistensi Notasi
Letak pembilang di atas garis dan penyebut di bawah garis telah menjadi notasi standar untuk pecahan. Konsistensi ini sangat penting untuk komunikasi matematika yang jelas dan menghindari kesalahpahaman.
Dengan demikian, letak pembilang di atas garis dan penyebut di bawah garis adalah aspek mendasar dari pecahan. Aspek ini memberikan dasar untuk membedakan pembilang dan penyebut, menunjukkan hubungan di antara keduanya, menentukan nilai pecahan, dan memastikan konsistensi notasi matematika.
Fungsi
Pembilang dan penyebut memainkan peran penting dalam menunjukkan nilai pecahan. Nilai pecahan ditentukan dengan membagi pembilang dengan penyebut. Pembilang mewakili jumlah bagian yang diambil dari keseluruhan, sedangkan penyebut mewakili jumlah bagian yang sama dalam keseluruhan. Dengan memahami hubungan ini, kita dapat menentukan nilai pecahan secara akurat.
-
Menunjukkan Bagian dari Keseluruhan
Pembilang menunjukkan jumlah bagian yang diambil dari keseluruhan. Misalnya, dalam pecahan 1/2, pembilang 1 menunjukkan bahwa satu bagian dari keseluruhan telah diambil. -
Menentukan Ukuran Bagian
Penyebut menunjukkan ukuran setiap bagian dalam keseluruhan. Dalam pecahan 1/2, penyebut 2 menunjukkan bahwa keseluruhan telah dibagi menjadi dua bagian yang sama. Dengan memahami ukuran bagian, kita dapat menentukan nilai pecahan. -
Menghitung Nilai Pecahan
Nilai pecahan dihitung dengan membagi pembilang dengan penyebut. Misalnya, nilai pecahan 1/2 dihitung dengan membagi 1 dengan 2, yang menghasilkan 0,5. Perhitungan ini memungkinkan kita untuk menentukan nilai pasti pecahan.
Dengan demikian, pembilang dan penyebut sangat penting untuk menunjukkan nilai pecahan. Mereka memungkinkan kita untuk memahami bagian dari keseluruhan yang diwakili oleh pecahan, menentukan ukuran setiap bagian, dan menghitung nilai pecahan secara akurat.
Perbandingan
Perbandingan merupakan aspek penting dalam memahami pecahan. Dengan membandingkan nilai pecahan, kita dapat menentukan pecahan mana yang lebih besar atau lebih kecil. Proses perbandingan ini sangat bergantung pada pembilang dan penyebut pecahan.
Nilai pecahan ditentukan dengan membagi pembilang dengan penyebut. Oleh karena itu, untuk membandingkan nilai pecahan, kita dapat melihat hubungan antara pembilang dan penyebut kedua pecahan.
Jika pembilang pecahan pertama lebih besar dari pembilang pecahan kedua dan penyebutnya sama, maka pecahan pertama lebih besar dari pecahan kedua. Sebaliknya, jika pembilang pecahan pertama lebih kecil dari pembilang pecahan kedua dan penyebutnya sama, maka pecahan pertama lebih kecil dari pecahan kedua.
Namun, jika pembilang kedua pecahan berbeda dan penyebutnya juga berbeda, maka kita perlu mencari nilai pecahan terlebih dahulu dengan membagi pembilang dengan penyebut. Setelah mendapatkan nilai pecahan, kita dapat membandingkan nilai tersebut untuk menentukan pecahan mana yang lebih besar atau lebih kecil.
Dengan demikian, perbandingan nilai pecahan sangat bergantung pada pembilang dan penyebut. Dengan memahami hubungan antara pembilang dan penyebut, kita dapat membandingkan nilai pecahan secara akurat dan menentukan urutannya.
Operasi
Pembilang dan penyebut memainkan peran penting dalam melakukan operasi matematika pada pecahan. Operasi-operasi ini meliputi penjumlahan, pengurangan, perkalian, dan pembagian pecahan.
Untuk melakukan operasi matematika pada pecahan, kita perlu memperhatikan pembilang dan penyebut masing-masing pecahan. Operasi-operasi tersebut dilakukan pada pembilang dan penyebut secara terpisah, dengan mempertimbangkan aturan-aturan matematika yang berlaku.
Kemampuan melakukan operasi matematika pada pecahan sangat penting untuk menyelesaikan berbagai masalah matematika. Operasi-operasi ini memungkinkan kita memanipulasi pecahan, membandingkan nilainya, dan menyelesaikan persamaan yang melibatkan pecahan.
Dengan demikian, pembilang dan penyebut menjadi komponen dasar dalam melakukan operasi matematika pada pecahan. Pemahaman yang baik tentang pembilang dan penyebut sangat penting untuk keberhasilan dalam operasi matematika yang melibatkan pecahan.
Sejarah
Konsep pembilang dan penyebut telah digunakan sejak zaman Babilonia, sekitar 4000 tahun yang lalu. Penggunaan awal ini menunjukkan pentingnya konsep pecahan dalam matematika dan relevansinya dalam berbagai bidang kehidupan.
-
Notasi Awal
Bangsa Babilonia menggunakan sistem bilangan seksagesimal (basis 60) dan mengembangkan sistem penulisan pecahan menggunakan simbol khusus untuk pembilang (bagian atas) dan penyebut (bagian bawah). Notasi ini menjadi dasar bagi notasi pecahan yang kita gunakan saat ini.
-
Aplikasi Praktis
Konsep pecahan digunakan oleh bangsa Babilonia untuk berbagai tujuan praktis, seperti pengukuran, pembagian sumber daya, dan perhitungan astronomi. Pemahaman tentang pembilang dan penyebut memungkinkan mereka untuk mewakili dan memanipulasi pecahan secara efektif.
-
Pengaruh pada Matematika
Penggunaan pembilang dan penyebut oleh bangsa Babilonia memiliki pengaruh yang signifikan pada perkembangan matematika. Konsep pecahan menjadi bagian integral dari sistem bilangan dan operasi matematika, membuka jalan bagi perkembangan aljabar dan kalkulus di kemudian hari.
Dengan demikian, sejarah penggunaan pembilang dan penyebut sejak zaman Babilonia menyoroti pentingnya konsep pecahan dalam matematika dan aplikasinya yang luas. Konsep ini terus menjadi dasar bagi operasi matematika dan pemecahan masalah hingga saat ini.
Jenis
Dalam matematika, pecahan dapat dinyatakan dalam berbagai bentuk, yaitu pecahan biasa, desimal, dan persen. Ketiga jenis pecahan ini memiliki keterkaitan dengan konsep pembilang dan penyebut.
-
Pecahan Biasa
Pecahan biasa terdiri dari pembilang dan penyebut yang dipisahkan oleh garis pemisah. Pembilang menunjukkan banyaknya bagian yang diambil dari keseluruhan, sedangkan penyebut menunjukkan banyaknya bagian yang sama dalam keseluruhan. -
Desimal
Desimal adalah bentuk pecahan yang dinyatakan dalam bentuk angka di belakang koma. Desimal dapat diperoleh dengan membagi pembilang pecahan biasa dengan penyebutnya. Dalam desimal, pembilang disebut angka di belakang koma, sedangkan penyebutnya adalah 10 pangkat banyaknya angka di belakang koma. -
Persen
Persen adalah bentuk pecahan yang menyatakan bagian dari seratus. Persen diperoleh dengan mengalikan pecahan biasa dengan 100. Dalam persen, pembilang disebut angka sebelum tanda persen, sedangkan penyebutnya adalah 100.
Meskipun memiliki bentuk yang berbeda, pecahan biasa, desimal, dan persen memiliki nilai yang sama. Ketiga jenis pecahan ini dapat dikonversi dari satu bentuk ke bentuk lainnya menggunakan operasi matematika yang sesuai.
Aplikasi
Pembilang dan penyebut memiliki peran penting dalam berbagai bidang di luar matematika, seperti sains, teknik, dan keuangan. Kemampuan untuk memahami dan memanipulasi pecahan sangat penting untuk memecahkan masalah dan membuat keputusan yang tepat di bidang-bidang ini.
-
Sains
Dalam sains, pecahan digunakan untuk menyatakan besaran fisik, seperti kecepatan, percepatan, dan konsentrasi. Pemahaman tentang pembilang dan penyebut memungkinkan para ilmuwan untuk membandingkan besaran ini, melakukan perhitungan, dan membuat prediksi berdasarkan data yang tersedia.
-
Teknik
Dalam teknik, pecahan digunakan dalam perancangan dan konstruksi. Insinyur menggunakan pecahan untuk menghitung beban, tegangan, dan efisiensi sistem. Pemahaman tentang pembilang dan penyebut sangat penting untuk memastikan keamanan dan keandalan struktur dan mesin.
-
Keuangan
Dalam keuangan, pecahan digunakan untuk menghitung suku bunga, persentase keuntungan, dan nilai investasi. Analis keuangan menggunakan pecahan untuk membuat keputusan investasi, mengelola risiko, dan merencanakan masa depan keuangan individu dan perusahaan.
-
Bidang Lainnya
Selain sains, teknik, dan keuangan, pecahan juga digunakan dalam berbagai bidang lain, seperti kesehatan, geografi, dan musik. Pemahaman tentang pembilang dan penyebut sangat penting untuk memahami konsep-konsep dasar dan melakukan perhitungan yang akurat di bidang-bidang ini.
Dengan demikian, pembilang dan penyebut merupakan konsep penting yang memiliki aplikasi luas di berbagai bidang. Kemampuan untuk memahami dan menggunakan pecahan secara efektif sangat penting untuk menguasai berbagai disiplin ilmu dan memecahkan masalah dunia nyata.
Pertanyaan Umum tentang Pecahan
Berikut adalah beberapa pertanyaan umum tentang pecahan beserta jawabannya:
Pertanyaan 1: Apa itu pecahan?
Pecahan adalah bilangan yang menyatakan bagian dari keseluruhan. Pecahan terdiri dari dua bagian, yaitu pembilang dan penyebut. Pembilang menunjukkan banyaknya bagian yang diambil, sedangkan penyebut menunjukkan banyaknya bagian yang sama dalam keseluruhan.
Pertanyaan 2: Bagaimana cara membandingkan pecahan?
Untuk membandingkan pecahan, kita bisa melihat nilai desimal atau persennya. Pecahan yang memiliki nilai desimal atau persen lebih besar, maka pecahan tersebut lebih besar nilainya.
Pertanyaan 3: Bagaimana cara menjumlahkan dan mengurangkan pecahan?
Untuk menjumlahkan atau mengurangkan pecahan, kita harus terlebih dahulu menyamakan penyebutnya. Setelah penyebutnya sama, kita bisa langsung menjumlahkan atau mengurangkan pembilangnya.
Pertanyaan 4: Bagaimana cara mengalikan dan membagi pecahan?
Untuk mengalikan pecahan, kita kalikan pembilang dengan pembilang dan penyebut dengan penyebut. Untuk membagi pecahan, kita balik pecahan kedua dan kemudian kalikan seperti biasa.
Dengan memahami konsep dasar pecahan, kita bisa menyelesaikan berbagai masalah matematika yang melibatkan pecahan dengan mudah dan akurat.
Kesimpulan
Pecahan merupakan konsep penting dalam matematika yang digunakan untuk menyatakan bagian dari keseluruhan. Dengan memahami pembilang dan penyebut, kita bisa membandingkan, menjumlahkan, mengurangkan, mengalikan, dan membagi pecahan dengan mudah.
Tips Memahami Pecahan
Pecahan merupakan konsep matematika yang penting untuk dikuasai. Berikut adalah beberapa tips untuk membantu Anda memahami pecahan:
Tip 1: Visualisasikan Pecahan
Bayangkan pecahan sebagai sebuah pizza yang dibagi menjadi beberapa bagian yang sama. Pembilang menunjukkan jumlah potongan pizza yang diambil, sedangkan penyebut menunjukkan jumlah total potongan pizza.
Tip 2: Sederhanakan Pecahan
Jika memungkinkan, sederhanakan pecahan dengan mencari faktor persekutuan terbesar (FPB) dari pembilang dan penyebut. Hal ini akan membuat pecahan lebih mudah untuk dihitung dan dibandingkan.
Tip 3: Bandingkan Pecahan
Untuk membandingkan dua pecahan, ubahlah pecahan tersebut menjadi pecahan desimal atau persen. Pecahan dengan nilai desimal atau persen yang lebih besar adalah pecahan yang lebih besar nilainya.
Tip 4: Operasikan Pecahan
Untuk menjumlahkan atau mengurangkan pecahan, samakan terlebih dahulu penyebutnya. Setelah penyebutnya sama, Anda dapat langsung menjumlahkan atau mengurangkan pembilangnya.
Tip 5: Pecahan Campuran
Pecahan campuran adalah pecahan yang terdiri dari bilangan bulat dan pecahan biasa. Untuk mengubah pecahan campuran menjadi pecahan biasa, kalikan bilangan bulat dengan penyebut, kemudian jumlahkan hasilnya dengan pembilang.
Dengan mengikuti tips ini, Anda dapat meningkatkan pemahaman Anda tentang pecahan dan menyelesaikan masalah matematika yang melibatkan pecahan dengan lebih mudah.
Kesimpulan
Pecahan adalah konsep penting dalam matematika yang digunakan untuk menyatakan bagian dari keseluruhan. Dengan memahami konsep pembilang dan penyebut, Anda dapat menguasai operasi pecahan dan menerapkannya dalam berbagai bidang kehidupan.
Youtube Video:










