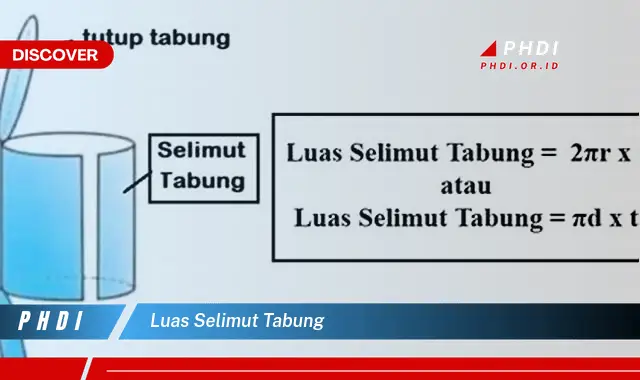
Luas selimut tabung adalah keliling alas tabung dikalikan dengan tinggi tabung. Luas selimut tabung memiliki rumus 2r x t, dimana adalah konstanta sekitar 3,14, r adalah jari-jari alas tabung, dan t adalah tinggi tabung. Misalnya, sebuah tabung dengan jari-jari alas 5 cm dan tinggi 10 cm memiliki luas selimut tabung 2 x 3,14 x 5 cm x 10 cm = 314 cm.
Luas selimut tabung penting dalam berbagai bidang, seperti teknik dan desain. Dalam teknik, luas selimut tabung digunakan untuk menghitung luas permukaan pipa atau tangki. Dalam desain, luas selimut tabung digunakan untuk menghitung luas permukaan benda-benda berbentuk tabung, seperti kaleng atau botol.
Konsep luas selimut tabung telah dikenal sejak zaman kuno. Ahli matematika Yunani Archimedes (287-212 SM) adalah salah satu orang pertama yang mempelajari luas selimut tabung. Ia mengembangkan rumus untuk luas selimut tabung yang masih digunakan sampai sekarang.
Luas Selimut Tabung
Luas selimut tabung merupakan aspek penting dalam berbagai bidang, seperti teknik dan desain. Berikut adalah 7 aspek penting terkait luas selimut tabung:
- Rumus: 2r x t
- Satuan: cm, m, dll
- Aplikasi: Menghitung luas permukaan pipa, tangki, kaleng
- Sejarah: Dikenal sejak zaman Archimedes
- Dimensi: Panjang x tinggi
- Bentuk: Tabung
- Jenis: Selimut tabung
Ketujuh aspek tersebut saling berkaitan dan membentuk pemahaman yang komprehensif tentang luas selimut tabung. Rumus luas selimut tabung digunakan untuk menghitung luas permukaan benda-benda berbentuk tabung, seperti pipa, tangki, dan kaleng. Satuan yang digunakan untuk menyatakan luas selimut tabung adalah cm, m, atau satuan luas lainnya. Pemahaman tentang dimensi dan bentuk luas selimut tabung sangat penting dalam aplikasi praktis, seperti desain dan teknik.
Rumus
Rumus 2r x t merupakan rumus yang digunakan untuk menghitung luas selimut tabung. Rumus ini diturunkan dari konsep keliling dan tinggi tabung. Keliling alas tabung dikalikan dengan tinggi tabung menghasilkan luas selimut tabung. Konstanta (pi) digunakan dalam rumus karena bentuk tabung yang melingkar.
Rumus 2r x t memiliki peran penting dalam menghitung luas selimut tabung karena memberikan metode yang akurat dan efisien untuk menentukan luas permukaan tabung. Tanpa rumus ini, menghitung luas selimut tabung akan menjadi proses yang rumit dan memakan waktu.
Sebagai komponen penting dari luas selimut tabung, rumus 2r x t memungkinkan kita untuk memahami dan menghitung luas permukaan tabung dengan cepat dan mudah. Rumus ini sangat penting dalam berbagai bidang, seperti teknik, desain, dan matematika.
Satuan
Satuan luas selimut tabung dinyatakan dalam cm, m, atau satuan luas lainnya. Satuan ini sangat penting karena menunjukkan ukuran luas selimut tabung. Tanpa satuan, luas selimut tabung tidak memiliki makna yang jelas dan tidak dapat digunakan untuk perhitungan lebih lanjut.
Pemilihan satuan yang tepat tergantung pada konteks dan tujuan perhitungan. Dalam teknik, satuan m biasanya digunakan untuk luas selimut tabung yang besar, seperti pipa atau tangki. Dalam desain, satuan cm lebih umum digunakan untuk luas selimut tabung yang lebih kecil, seperti kaleng atau botol.
Satuan luas selimut tabung juga penting untuk konversi antar satuan. Misalnya, jika luas selimut tabung diberikan dalam cm dan kita ingin mengonversinya ke m, kita perlu membagi nilai tersebut dengan 10.000.
Aplikasi
Salah satu aplikasi terpenting dari luas selimut tabung adalah untuk menghitung luas permukaan pipa, tangki, dan kaleng. Benda-benda ini memiliki bentuk tabung, sehingga luas permukaannya dapat dihitung menggunakan rumus luas selimut tabung, yaitu 2r x t.
Menghitung luas permukaan pipa, tangki, dan kaleng sangat penting dalam berbagai bidang. Dalam teknik, luas permukaan pipa diperlukan untuk menghitung kehilangan panas dan menentukan ukuran insulasi yang tepat. Dalam desain, luas permukaan tangki digunakan untuk menentukan kapasitas dan bentuk tangki yang optimal. Dalam industri pengemasan, luas permukaan kaleng digunakan untuk menghitung biaya bahan dan menentukan desain label.
Sejarah
Konsep luas selimut tabung telah dikenal sejak zaman Archimedes, seorang ahli matematika Yunani yang hidup pada abad ke-3 SM. Archimedes mengembangkan rumus untuk luas selimut tabung, yang masih digunakan hingga sekarang. Rumus ini merupakan dasar dari perhitungan luas selimut tabung dan telah memainkan peran penting dalam pengembangan matematika dan teknik.
Pengaruh Archimedes pada konsep luas selimut tabung sangatlah signifikan. Rumusnya memberikan dasar yang kuat untuk menghitung luas permukaan tabung, yang sangat penting dalam berbagai bidang seperti teknik, desain, dan fisika. Tanpa kontribusi Archimedes, pemahaman kita tentang luas selimut tabung akan jauh berbeda dan kemajuan dalam bidang-bidang ini akan terhambat.
Dimensi
Dimensi luas selimut tabung adalah panjang x tinggi. Panjang mewakili keliling alas tabung, sedangkan tinggi mewakili tinggi tabung. Kedua dimensi ini sangat penting dalam menentukan luas selimut tabung karena merupakan faktor perkalian dalam rumus luas selimut tabung, yaitu 2r x t.
Perubahan pada panjang atau tinggi tabung akan berdampak langsung pada luas selimut tabung. Jika panjang tabung bertambah, maka luas selimut tabung juga akan bertambah. Demikian pula, jika tinggi tabung bertambah, maka luas selimut tabung juga akan bertambah. Hubungan ini menunjukkan bahwa dimensi panjang x tinggi sangat penting sebagai komponen luas selimut tabung.
Memahami dimensi panjang x tinggi sangat penting untuk menghitung luas selimut tabung secara akurat. Tanpa dimensi ini, tidak mungkin untuk menentukan luas permukaan tabung, yang sangat penting dalam berbagai aplikasi, seperti teknik, desain, dan fisika.
Bentuk
Bentuk tabung merupakan aspek penting dari konsep luas selimut tabung. Tabung adalah bangun ruang tiga dimensi yang memiliki dua sisi datar berbentuk lingkaran yang sejajar dan sebuah sisi lengkung yang menghubungkan kedua sisi datar tersebut. Luas selimut tabung adalah luas permukaan sisi lengkung tabung.
-
Komponen Tabung
Tabung terdiri dari beberapa komponen, yaitu jari-jari alas (r), tinggi (t), dan keliling alas (2r). Ketiga komponen ini berperan penting dalam menghitung luas selimut tabung.
-
Contoh Tabung
Dalam kehidupan nyata, tabung banyak ditemukan dalam berbagai bentuk, seperti pipa, kaleng, dan botol. Bentuk-bentuk ini memiliki ciri khas sisi lengkung yang membedakannya dari bangun ruang lainnya.
Memahami bentuk tabung sangat penting untuk menghitung luas selimut tabung secara akurat. Tanpa pemahaman yang baik tentang bentuk tabung, akan sulit untuk menerapkan rumus luas selimut tabung dengan benar. Selain itu, pemahaman tentang bentuk tabung juga penting dalam berbagai aplikasi, seperti teknik, desain, dan fisika.
Jenis
Selimut tabung merupakan jenis permukaan tabung yang memiliki sifat dan karakteristik khusus. Jenis permukaan ini memegang peranan penting dalam menentukan luas selimut tabung.
Luas selimut tabung adalah luas permukaan sisi lengkung tabung, tidak termasuk luas permukaan kedua sisi datar. Sisi lengkung tabung inilah yang disebut sebagai selimut tabung. Oleh karena itu, jenis permukaan selimut tabung sangat memengaruhi luas selimut tabung secara keseluruhan.
Sifat khas selimut tabung adalah memiliki bentuk lengkung yang menghubungkan kedua sisi datar tabung. Luas permukaan selimut tabung bergantung pada keliling alas dan tinggi tabung. Semakin besar keliling alas dan tinggi tabung, maka semakin besar pula luas selimut tabung.
Tanya Jawab Luas Selimut Tabung
Bagian ini menyajikan tanya jawab umum terkait luas selimut tabung untuk memberikan pemahaman yang lebih komprehensif.
Pertanyaan 1: Apa yang dimaksud dengan luas selimut tabung?
Luas selimut tabung adalah luas permukaan sisi lengkung tabung, tidak termasuk luas permukaan kedua sisi datar. Sisi lengkung tabung inilah yang disebut sebagai selimut tabung.
Pertanyaan 2: Bagaimana cara menghitung luas selimut tabung?
Luas selimut tabung dapat dihitung menggunakan rumus:Luas selimut tabung = 2 x x r x tdi mana:- adalah konstanta sekitar 3,14- r adalah jari-jari alas tabung- t adalah tinggi tabung
Pertanyaan 3: Apa saja aplikasi luas selimut tabung?
Luas selimut tabung memiliki berbagai aplikasi dalam bidang teknik, desain, dan fisika, seperti:- Menghitung luas permukaan pipa, tangki, dan kaleng- Menentukan kapasitas dan bentuk tangki yang optimal- Menghitung kehilangan panas pada pipa
Pertanyaan 4: Faktor apa saja yang memengaruhi luas selimut tabung?
Luas selimut tabung dipengaruhi oleh dua faktor utama, yaitu jari-jari alas tabung (r) dan tinggi tabung (t). Semakin besar jari-jari alas atau tinggi tabung, maka semakin besar pula luas selimut tabung.
Dengan memahami konsep dan aplikasi luas selimut tabung, kita dapat menyelesaikan berbagai permasalahan yang melibatkan bangun ruang tabung dengan lebih efektif dan akurat.
Selanjutnya, kita akan membahas topik yang berkaitan dengan luas selimut tabung…
Tips Menghitung Luas Selimut Tabung
Untuk menghitung luas selimut tabung secara akurat dan efisien, berikut beberapa tips yang dapat diterapkan:
Tip 1: Pastikan satuan yang digunakan konsisten
Satuan yang digunakan untuk jari-jari alas, tinggi tabung, dan luas selimut tabung harus konsisten. Misalnya, jika jari-jari alas dan tinggi tabung menggunakan satuan sentimeter, maka luas selimut tabung juga harus dinyatakan dalam satuan sentimeter persegi.
Tip 2: Gunakan nilai yang tepat
Konstanta bernilai sekitar 3,14. Dalam perhitungan, gunakan nilai yang tepat untuk memastikan akurasi hasil.
Tip 3: Identifikasi jari-jari alas dan tinggi tabung dengan benar
Dalam rumus luas selimut tabung, r mewakili jari-jari alas dan t mewakili tinggi tabung. Pastikan untuk mengidentifikasi dan menggunakan nilai yang benar untuk kedua variabel ini.
Tip 4: Verifikasi hasil perhitungan
Setelah menyelesaikan perhitungan, verifikasi kembali hasil yang diperoleh dengan menggunakan kalkulator atau dengan memeriksa kembali langkah-langkah perhitungan.
Tip 5: Pahami konsep luas selimut tabung
Luas selimut tabung adalah luas permukaan sisi lengkung tabung, tidak termasuk luas permukaan kedua sisi datar. Memahami konsep ini akan membantu dalam menyelesaikan permasalahan yang melibatkan luas selimut tabung.
Dengan mengikuti tips ini, Anda dapat menghitung luas selimut tabung dengan lebih mudah, akurat, dan efisien.
Ingat, luas selimut tabung adalah aspek penting dalam berbagai bidang, seperti teknik, desain, dan fisika. Dengan memahami konsep dan tips ini, Anda dapat menguasai perhitungan luas selimut tabung dan menerapkannya dalam berbagai aplikasi praktis.
Youtube Video:










