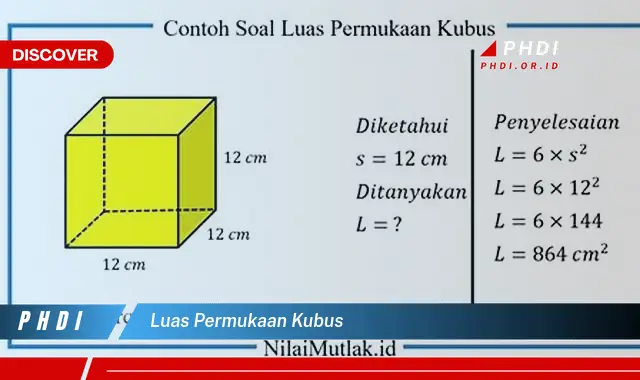
Luas permukaan kubus adalah jumlah luas semua sisi kubus. Untuk menghitung luas permukaan kubus, kita perlu mengalikan luas salah satu sisinya dengan 6. Misalnya, jika panjang sisi kubus adalah 5 cm, maka luas permukaan kubusnya adalah 6 x 5 x 5 = 150 cm persegi.
Mengetahui luas permukaan kubus penting dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Luas permukaan kubus dapat digunakan untuk menghitung jumlah bahan yang dibutuhkan untuk membuat sebuah kubus, serta untuk menghitung luas permukaan benda-benda yang berbentuk kubus.
Konsep luas permukaan kubus pertama kali diperkenalkan oleh matematikawan Yunani kuno, Euclid, dalam bukunya “Elements”. Euclid menggunakan luas permukaan kubus untuk membuktikan beberapa teorema geometri, seperti Teorema Pythagoras.
Luas Permukaan Kubus
Luas permukaan kubus adalah besaran yang penting dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Berikut adalah 7 aspek penting terkait luas permukaan kubus:
- Definisi: Jumlah luas semua sisi kubus.
- Rumus: 6 x (panjang sisi)^2.
- Satuan: Satuan luas, seperti cm persegi atau m persegi.
- Aplikasi: Menghitung kebutuhan bahan dan luas permukaan benda berbentuk kubus.
- Sejarah: Diperkenalkan pertama kali oleh Euclid dalam “Elements”.
- Teorema: Digunakan untuk membuktikan teorema geometri, seperti Teorema Pythagoras.
- Pentingnya: Dasar untuk perhitungan yang lebih kompleks dalam bidang matematika dan sains.
Dengan memahami aspek-aspek penting ini, kita dapat memperoleh pemahaman yang lebih komprehensif tentang luas permukaan kubus dan relevansinya dalam berbagai bidang.
Definisi
Definisi tersebut mengacu pada konsep dasar luas permukaan kubus, yang merupakan jumlah luas semua sisi yang menyusun kubus tersebut. Pemahaman tentang definisi ini sangat penting untuk memahami konsep luas permukaan kubus secara keseluruhan dan penerapannya dalam berbagai bidang.
-
Komponen penyusun
Setiap kubus terdiri dari enam sisi berbentuk persegi yang identik. Luas permukaan kubus diperoleh dengan menjumlahkan luas keenam sisi tersebut.
-
Contoh penerapan
Dalam arsitektur, luas permukaan kubus digunakan untuk menghitung luas permukaan bangunan yang berbentuk kubus, seperti rumah atau gedung perkantoran.
-
Implikasi dalam konteks luas permukaan kubus
Definisi tersebut menyiratkan bahwa luas permukaan kubus berbanding lurus dengan luas salah satu sisinya. Jika luas sisi kubus diperbesar, maka luas permukaan kubusnya juga akan membesar.
Dengan memahami definisi dan implikasinya, kita dapat memperoleh pemahaman yang lebih komprehensif tentang konsep luas permukaan kubus dan relevansinya dalam berbagai bidang.
Rumus
Rumus tersebut merupakan persamaan matematika yang digunakan untuk menghitung luas permukaan kubus. Rumus ini menyatakan bahwa luas permukaan kubus sama dengan enam kali kuadrat panjang sisinya. Dengan kata lain, untuk menghitung luas permukaan kubus, kita perlu mengalikan luas salah satu sisinya dengan 6.
Rumus ini sangat penting karena memungkinkan kita untuk menghitung luas permukaan kubus dengan mudah dan cepat. Tanpa rumus ini, kita perlu menghitung luas setiap sisi kubus secara terpisah, kemudian menjumlahkannya untuk mendapatkan luas permukaan total. Rumus ini juga memungkinkan kita untuk menggeneralisasi perhitungan luas permukaan kubus, sehingga kita dapat menghitung luas permukaan kubus dengan ukuran berapa pun.
Selain itu, rumus ini memiliki implikasi penting dalam memahami sifat-sifat luas permukaan kubus. Misalnya, rumus ini menunjukkan bahwa luas permukaan kubus berbanding lurus dengan kuadrat panjang sisinya. Artinya, jika panjang sisi kubus diperbesar dua kali, maka luas permukaan kubusnya akan menjadi empat kali lebih besar.
Satuan
Satuan luas sangat penting dalam konteks luas permukaan kubus karena memungkinkan kita untuk mengukur dan membandingkan luas permukaan kubus yang berbeda. Satuan luas yang umum digunakan untuk mengukur luas permukaan kubus antara lain sentimeter persegi (cm persegi) dan meter persegi (m persegi).
Penggunaan satuan luas yang tepat sangat penting untuk memastikan keakuratan dan konsistensi dalam pengukuran luas permukaan kubus. Misalnya, jika kita mengukur luas permukaan kubus dalam sentimeter persegi, maka hasil pengukurannya akan berbeda jika kita mengukur luas permukaan kubus yang sama dalam meter persegi.
Selain itu, satuan luas juga memungkinkan kita untuk mengonversi luas permukaan kubus dari satu satuan ke satuan lainnya. Misalnya, jika kita mengetahui luas permukaan kubus dalam sentimeter persegi, kita dapat mengonversinya ke meter persegi dengan membagi luas permukaan kubus tersebut dengan 10.000.
Aplikasi
Salah satu aplikasi penting dari luas permukaan kubus adalah untuk menghitung kebutuhan bahan dan luas permukaan benda berbentuk kubus. Dalam berbagai bidang, seperti arsitektur dan teknik, menghitung kebutuhan bahan dan luas permukaan benda berbentuk kubus merupakan hal yang penting untuk perencanaan dan penganggaran.
Dengan mengetahui luas permukaan kubus, kita dapat menghitung jumlah bahan yang dibutuhkan untuk membuat benda tersebut. Misalnya, jika kita ingin membuat sebuah kotak berbentuk kubus, kita perlu mengetahui luas permukaan kubus tersebut untuk menentukan jumlah bahan, seperti kayu atau logam, yang dibutuhkan untuk membuat kotak tersebut.
Selain itu, luas permukaan kubus juga penting untuk menghitung luas permukaan benda berbentuk kubus. Luas permukaan benda berbentuk kubus diperlukan dalam berbagai aplikasi, seperti pengecatan, pelapisan, dan desain interior. Dengan mengetahui luas permukaan benda berbentuk kubus, kita dapat memperkirakan jumlah bahan yang dibutuhkan untuk melapisi atau mengecat benda tersebut.
Sejarah
Sejarah penemuan luas permukaan kubus tidak dapat dilepaskan dari peran penting matematikawan Yunani kuno, Euclid, yang hidup pada abad ke-3 SM. Euclid memperkenalkan konsep luas permukaan kubus dalam karyanya yang terkenal, “Elements”. “Elements” merupakan sebuah risalah matematika yang berisi 13 buku, dan buku ke-12 membahas tentang geometri bangun ruang, termasuk kubus.
Dalam “Elements”, Euclid membuktikan beberapa teorema penting terkait kubus, termasuk teorema yang menyatakan bahwa luas permukaan kubus sama dengan enam kali luas salah satu sisinya. Teorema ini menjadi dasar bagi rumus luas permukaan kubus yang kita gunakan hingga sekarang.
Pengenalan konsep luas permukaan kubus oleh Euclid dalam “Elements” memiliki dampak yang sangat signifikan terhadap perkembangan matematika dan sains. Konsep ini menjadi dasar bagi banyak teorema dan aplikasi penting dalam geometri, arsitektur, dan teknik.
Teorema
Konsep luas permukaan kubus memiliki hubungan yang erat dengan teorema-teorema geometri, termasuk Teorema Pythagoras. Teorema-teorema ini digunakan untuk membuktikan sifat-sifat dan hubungan antara berbagai bangun geometri, termasuk kubus.
-
Bukti sifat-sifat kubus
Luas permukaan kubus digunakan dalam pembuktian berbagai sifat kubus, seperti sifat diagonal ruang dan diagonal bidang. Sifat-sifat ini penting dalam memahami geometri kubus dan penerapannya dalam bidang-bidang seperti arsitektur dan teknik.
-
Aplikasi dalam kehidupan nyata
Konsep luas permukaan kubus dan teorema-teorema geometri terkait digunakan dalam berbagai aplikasi kehidupan nyata, seperti desain furnitur, arsitektur, dan teknik sipil. Misalnya, dalam arsitektur, luas permukaan kubus digunakan untuk menghitung luas permukaan bangunan dan menentukan kebutuhan bahan bangunan.
-
Dasar pengembangan matematika
Teorema-teorema geometri yang berkaitan dengan luas permukaan kubus menjadi dasar pengembangan konsep matematika yang lebih kompleks, seperti kalkulus dan geometri analitik. Konsep-konsep ini sangat penting dalam berbagai bidang sains dan teknologi.
Dengan memahami hubungan antara luas permukaan kubus dan teorema-teorema geometri, kita dapat memperoleh pemahaman yang lebih komprehensif tentang sifat-sifat dan aplikasi kubus dalam berbagai bidang.
Pentingnya
Konsep luas permukaan kubus memainkan peran penting sebagai dasar untuk perhitungan yang lebih kompleks dalam berbagai bidang matematika dan sains. Berikut adalah beberapa alasannya:
-
Geometri dan Trigonometri
Luas permukaan kubus digunakan dalam perhitungan volume dan luas permukaan bangun ruang lainnya, seperti prisma dan limas. Konsep ini juga menjadi dasar dalam pengembangan teorema dan rumus geometri, seperti Teorema Pythagoras dan rumus volume kubus. -
Kalkulus
Luas permukaan kubus merupakan salah satu bentuk dasar integral. Pemahaman tentang luas permukaan kubus sangat penting untuk memahami konsep integral dan penerapannya dalam kalkulus. -
Fisika dan Teknik
Luas permukaan kubus digunakan dalam perhitungan gaya, tekanan, dan perpindahan panas. Konsep ini sangat penting dalam bidang teknik, seperti teknik mesin dan teknik sipil, untuk merancang dan menganalisis berbagai struktur dan sistem.
Dengan demikian, konsep luas permukaan kubus menjadi fondasi yang penting untuk pengembangan dan penerapan matematika dan sains dalam berbagai bidang.
Pertanyaan Umum tentang Luas Permukaan Kubus
Berikut adalah beberapa pertanyaan umum tentang luas permukaan kubus, beserta jawabannya:
Pertanyaan 1: Bagaimana cara menghitung luas permukaan kubus?
Jawaban: Luas permukaan kubus dapat dihitung dengan menggunakan rumus: 6 x (panjang sisi)^2, di mana panjang sisi adalah panjang salah satu sisi kubus.
Pertanyaan 2: Apa satuan yang digunakan untuk menyatakan luas permukaan kubus?
Jawaban: Satuan yang digunakan untuk menyatakan luas permukaan kubus adalah satuan luas, seperti sentimeter persegi (cm^2) atau meter persegi (m^2).
Pertanyaan 3: Mengapa penting untuk mengetahui luas permukaan kubus?
Jawaban: Luas permukaan kubus penting untuk berbagai aplikasi, seperti menghitung kebutuhan bahan untuk membuat benda berbentuk kubus, menghitung luas permukaan benda berbentuk kubus, dan menghitung volume kubus.
Pertanyaan 4: Bagaimana konsep luas permukaan kubus digunakan dalam matematika dan sains?
Jawaban: Konsep luas permukaan kubus digunakan sebagai dasar untuk perhitungan yang lebih kompleks dalam bidang matematika dan sains, seperti geometri, kalkulus, fisika, dan teknik.
Kesimpulan
Dengan memahami konsep luas permukaan kubus dan jawaban atas pertanyaan umum ini, kita dapat memperoleh pemahaman yang lebih komprehensif tentang sifat-sifat kubus dan relevansinya dalam berbagai bidang.
Bagian Artikel Selanjutnya
Tips Memahami Luas Permukaan Kubus
Berikut adalah beberapa tips untuk membantu Anda memahami luas permukaan kubus:
Tip 1: Visualisasikan Kubus
Bayangkan sebuah kubus sebagai sebuah kotak dengan enam sisi berbentuk persegi. Setiap sisi memiliki ukuran yang sama.
Tip 2: Pahami Rumus Luas Permukaan Kubus
Luas permukaan kubus dapat dihitung menggunakan rumus: 6 x (panjang sisi)^2, di mana panjang sisi adalah panjang salah satu sisi kubus.
Tip 3: Hitung Luas Salah Satu Sisi
Untuk menghitung luas permukaan kubus, Anda perlu terlebih dahulu menghitung luas salah satu sisinya. Luas persegi adalah panjang sisi x panjang sisi.
Tip 4: Kalikan dengan 6
Setelah Anda mengetahui luas salah satu sisi, kalikan dengan 6 untuk mendapatkan luas permukaan kubus.
Tip 5: Gunakan Satuan yang Benar
Saat menyatakan luas permukaan kubus, pastikan Anda menggunakan satuan yang benar, seperti sentimeter persegi (cm^2) atau meter persegi (m^2).
Kesimpulan
Dengan mengikuti tips ini, Anda dapat lebih mudah memahami konsep luas permukaan kubus dan menerapkannya dalam berbagai aplikasi.
Youtube Video:










