KPK dan FPB adalah dua konsep dasar dalam matematika yang digunakan untuk mencari kelipatan persekutuan terkecil (KPK) dan faktor persekutuan terbesar (FPB) dari dua bilangan atau lebih.
KPK adalah bilangan terkecil yang habis dibagi oleh kedua bilangan tersebut. Sedangkan FPB adalah bilangan terbesar yang membagi kedua bilangan tersebut tanpa sisa.
Konsep KPK dan FPB sangat penting dalam berbagai bidang matematika, seperti aljabar, geometri, dan teori bilangan. Konsep ini juga digunakan dalam aplikasi praktis, seperti mencari waktu paling singkat yang dibutuhkan agar dua peristiwa terjadi bersamaan atau menentukan ukuran terkecil yang dapat dibagi rata oleh beberapa objek.
KPK dan FPB
KPK dan FPB merupakan konsep dasar matematika yang penting untuk dipahami. Berikut adalah tujuh aspek penting terkait KPK dan FPB:
- Definisi: KPK adalah kelipatan persekutuan terkecil, sedangkan FPB adalah faktor persekutuan terbesar.
- Penghitungan: KPK dapat dihitung dengan mengalikan semua faktor prima yang sama dan berlainan dari kedua bilangan, sedangkan FPB dapat dihitung dengan mengalikan semua faktor prima yang sama dari kedua bilangan.
- Sifat: KPK dan FPB selalu positif dan merupakan bilangan bulat. KPK selalu lebih besar atau sama dengan FPB.
- Aplikasi: KPK dan FPB banyak digunakan dalam berbagai bidang, seperti mencari waktu paling singkat yang dibutuhkan agar dua peristiwa terjadi bersamaan atau menentukan ukuran terkecil yang dapat dibagi rata oleh beberapa objek.
- Aljabar: KPK dan FPB digunakan untuk menyederhanakan pecahan aljabar dan menyelesaikan persamaan.
- Geometri: KPK dan FPB digunakan untuk mencari luas dan volume bangun ruang.
- Teori Bilangan: KPK dan FPB digunakan untuk mempelajari sifat-sifat bilangan.
Pemahaman tentang KPK dan FPB sangat penting untuk menguasai matematika dasar. Konsep ini juga memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti dalam bidang teknik, fisika, dan ekonomi.
Definisi
Definisi ini merupakan dasar untuk memahami konsep KPK dan FPB. KPK adalah bilangan terkecil yang habis dibagi oleh kedua bilangan yang diberikan, sedangkan FPB adalah bilangan terbesar yang membagi kedua bilangan tersebut tanpa sisa. Pengertian ini sangat penting karena menjadi landasan bagi semua operasi dan aplikasi KPK dan FPB.
-
Sifat-sifat KPK dan FPB
Dari definisi tersebut, dapat diturunkan beberapa sifat penting KPK dan FPB, seperti KPK selalu lebih besar atau sama dengan FPB, KPK dan FPB selalu positif, dan KPK dan FPB dari dua bilangan yang sama adalah bilangan itu sendiri. Pemahaman tentang sifat-sifat ini sangat penting untuk menyelesaikan berbagai permasalahan yang melibatkan KPK dan FPB.
-
Penghitungan KPK dan FPB
Definisi KPK dan FPB juga menjadi dasar untuk menghitung KPK dan FPB dari dua bilangan atau lebih. Ada beberapa metode yang dapat digunakan untuk menghitung KPK dan FPB, seperti metode faktorisasi prima dan metode bagi bersusun. Pemilihan metode yang tepat tergantung pada bilangan yang diberikan dan tingkat kesulitan soal.
-
Aplikasi KPK dan FPB
Pemahaman tentang KPK dan FPB sangat penting karena memiliki banyak aplikasi dalam kehidupan sehari-hari. Misalnya, KPK digunakan untuk mencari waktu paling singkat yang dibutuhkan agar dua peristiwa terjadi bersamaan, sedangkan FPB digunakan untuk menentukan ukuran terkecil yang dapat dibagi rata oleh beberapa objek.
Dengan memahami definisi KPK dan FPB, kita dapat menguasai konsep dasar ini dan menerapkannya untuk menyelesaikan berbagai permasalahan matematika dan kehidupan sehari-hari.
Penghitungan
Penghitungan KPK dan FPB merupakan aspek penting dalam memahami konsep KPK dan FPB. Metode penghitungan yang dijelaskan di atas memberikan langkah-langkah sistematis untuk menentukan KPK dan FPB dari dua bilangan atau lebih. Metode ini didasarkan pada konsep faktorisasi prima, yaitu menguraikan bilangan menjadi hasil kali faktor-faktor primanya.
-
Faktorisasi Prima
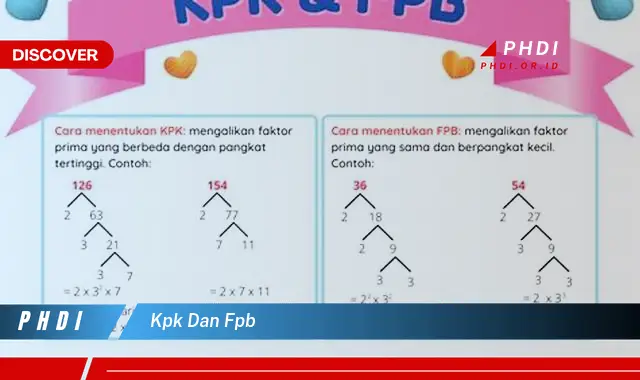
Faktorisasi prima adalah kunci dalam menghitung KPK dan FPB. Dengan memfaktorkan kedua bilangan menjadi faktor-faktor primanya, kita dapat mengidentifikasi faktor-faktor prima yang sama dan berlainan. Faktor-faktor prima yang sama digunakan untuk menghitung FPB, sedangkan faktor-faktor prima yang berbeda digunakan untuk menghitung KPK.
-
Mengalikan Faktor Prima
Setelah memfaktorkan kedua bilangan, langkah selanjutnya adalah mengalikan faktor-faktor prima yang sesuai. Untuk menghitung KPK, kita mengalikan semua faktor prima yang sama dan berlainan. Sedangkan untuk menghitung FPB, kita hanya mengalikan faktor-faktor prima yang sama.
-
Contoh
Misalnya, untuk mencari KPK dan FPB dari 12 dan 18, kita faktorkan kedua bilangan tersebut: 12 = 2 x 2 x 3 dan 18 = 2 x 3 x 3. Faktor prima yang sama adalah 2 dan 3. Untuk KPK, kita mengalikan semua faktor prima, yaitu 2 x 2 x 3 x 3 = 36. Sedangkan untuk FPB, kita hanya mengalikan faktor prima yang sama, yaitu 2 x 3 = 6.
Dengan memahami metode penghitungan KPK dan FPB, kita dapat menyelesaikan berbagai permasalahan matematika dan kehidupan sehari-hari yang melibatkan KPK dan FPB.
Sifat
Sifat-sifat KPK dan FPB tersebut sangat penting karena menjadi dasar bagi operasi dan aplikasi KPK dan FPB. Sifat KPK yang selalu lebih besar atau sama dengan FPB menunjukkan bahwa KPK adalah kelipatan bersama terkecil yang dapat dibagi oleh kedua bilangan, sedangkan FPB adalah faktor persekutuan terbesar yang membagi kedua bilangan tanpa sisa. Sifat KPK dan FPB yang selalu positif menunjukkan bahwa KPK dan FPB selalu merupakan bilangan asli, bukan bilangan negatif atau nol. Sifat-sifat ini juga menjadi dasar bagi pembuktian sifat-sifat KPK dan FPB lainnya, seperti sifat distributif, asosiatif, dan komutatif. Dengan memahami sifat-sifat KPK dan FPB, kita dapat menggunakannya secara efektif untuk menyelesaikan berbagai permasalahan matematika.
Aplikasi
KPK dan FPB memiliki banyak aplikasi dalam berbagai bidang kehidupan. Salah satu aplikasi penting adalah untuk mencari waktu paling singkat yang dibutuhkan agar dua peristiwa terjadi bersamaan atau menentukan ukuran terkecil yang dapat dibagi rata oleh beberapa objek. Konsep KPK dan FPB dapat membantu kita memecahkan masalah sehari-hari secara efektif dan efisien.
-
Mencari Waktu Paling Singkat
KPK dapat digunakan untuk menentukan waktu paling singkat yang dibutuhkan agar dua peristiwa terjadi bersamaan. Misalnya, jika seorang siswa memiliki jadwal les matematika setiap 6 hari dan les bahasa Inggris setiap 8 hari, maka KPK dari 6 dan 8 adalah 24. Artinya, kedua les tersebut akan bersamaan setiap 24 hari.
-
Menentukan Ukuran Terkecil
FPB dapat digunakan untuk menentukan ukuran terkecil yang dapat dibagi rata oleh beberapa objek. Misalnya, jika kita ingin mengemas 12 buku dan 15 pensil ke dalam beberapa kotak dengan ukuran yang sama, maka FPB dari 12 dan 15 adalah 3. Artinya, kita dapat mengemas buku dan pensil tersebut ke dalam kotak-kotak berukuran 3, 6, 9, atau kelipatan 3 lainnya.
Selain aplikasi tersebut, KPK dan FPB juga banyak digunakan dalam bidang lainnya, seperti fisika, teknik, dan ekonomi. Pemahaman tentang KPK dan FPB sangat penting untuk menyelesaikan berbagai masalah dalam kehidupan sehari-hari dan bidang keilmuan secara efektif dan efisien.
Aljabar
Dalam aljabar, KPK dan FPB memainkan peran penting dalam menyederhanakan pecahan aljabar dan menyelesaikan persamaan. Hubungan antara keduanya adalah sebagai berikut:
-
Menyederhanakan Pecahan Aljabar
KPK digunakan untuk menyederhanakan pecahan aljabar dengan mencari penyebut yang sama untuk semua suku. Dengan menggunakan KPK sebagai penyebut, pecahan aljabar dapat disederhanakan dan dioperasikan dengan lebih mudah.
-
Menyelesaikan Persamaan
KPK dan FPB digunakan untuk menyelesaikan persamaan yang melibatkan pecahan aljabar. KPK digunakan untuk menghilangkan penyebut pada kedua sisi persamaan, sedangkan FPB digunakan untuk menyederhanakan pembilang pada kedua sisi persamaan. Dengan demikian, persamaan dapat diselesaikan dengan lebih mudah.
Pemahaman tentang KPK dan FPB sangat penting dalam aljabar karena konsep ini memungkinkan kita untuk menyederhanakan dan menyelesaikan berbagai jenis ekspresi aljabar. Penguasaan KPK dan FPB akan membantu siswa untuk memahami dan menyelesaikan masalah aljabar dengan lebih efektif dan efisien.
Geometri
Konsep KPK dan FPB sangat penting dalam geometri untuk mencari luas dan volume bangun ruang. Hubungan antara keduanya adalah sebagai berikut:
-
Mencari Luas Bangun Datar
KPK dan FPB digunakan untuk mencari luas bangun datar yang tersusun dari beberapa bangun datar. Misalnya, untuk mencari luas persegi panjang yang tersusun dari beberapa persegi kecil, kita dapat menggunakan KPK dari panjang dan lebar persegi untuk mencari luas keseluruhan.
-
Mencari Volume Bangun Ruang
KPK dan FPB juga digunakan untuk mencari volume bangun ruang yang tersusun dari beberapa bangun ruang. Misalnya, untuk mencari volume balok yang tersusun dari beberapa kubus kecil, kita dapat menggunakan KPK dari panjang, lebar, dan tinggi kubus untuk mencari volume keseluruhan.
Pemahaman tentang KPK dan FPB sangat penting dalam geometri karena konsep ini memungkinkan kita untuk mencari luas dan volume bangun ruang yang kompleks dengan lebih mudah dan efisien. Penguasaan KPK dan FPB akan membantu siswa untuk memahami dan menyelesaikan masalah geometri dengan lebih efektif.
Teori Bilangan
Teori bilangan adalah cabang matematika yang mempelajari sifat-sifat bilangan. Salah satu konsep penting dalam teori bilangan adalah KPK dan FPB, yang dapat digunakan untuk memahami berbagai sifat bilangan.
-
Mengidentifikasi Bilangan Prima
KPK dan FPB dapat digunakan untuk mengidentifikasi bilangan prima. Bilangan prima adalah bilangan asli yang hanya memiliki dua faktor, yaitu 1 dan bilangan itu sendiri. Jika FPB dari dua bilangan adalah 1, maka kedua bilangan tersebut adalah bilangan prima.
-
Mencari Faktor Bilangan
KPK dan FPB dapat digunakan untuk mencari faktor-faktor suatu bilangan. Faktor suatu bilangan adalah bilangan asli yang membagi bilangan tersebut tanpa sisa. KPK dari suatu bilangan dan semua faktornya adalah bilangan itu sendiri, sedangkan FPB dari suatu bilangan dan semua faktornya adalah 1.
-
Menyederhanakan Pecahan
KPK dan FPB dapat digunakan untuk menyederhanakan pecahan. KPK dari pembilang dan penyebut suatu pecahan adalah penyebut terkecil yang dapat digunakan untuk menulis pecahan tersebut. FPB dari pembilang dan penyebut suatu pecahan adalah pembilang terbesar yang dapat digunakan untuk menulis pecahan tersebut.
-
Menyelesaikan Persamaan Diofanta
KPK dan FPB dapat digunakan untuk menyelesaikan persamaan Diofanta. Persamaan Diofanta adalah persamaan yang semua variabelnya adalah bilangan bulat. KPK dan FPB dapat digunakan untuk menemukan solusi bilangan bulat dari persamaan Diofanta.
Pemahaman tentang KPK dan FPB sangat penting dalam teori bilangan karena konsep ini memungkinkan kita untuk mempelajari dan memahami sifat-sifat bilangan dengan lebih dalam dan komprehensif. Penguasaan KPK dan FPB akan membantu siswa untuk memahami dan menyelesaikan masalah teori bilangan dengan lebih efektif dan efisien.
Pertanyaan Umum tentang KPK dan FPB
Konsep KPK dan FPB merupakan hal mendasar dalam matematika yang banyak digunakan dalam berbagai bidang. Berikut adalah beberapa pertanyaan umum dan jawabannya untuk membantu pemahaman yang lebih baik tentang KPK dan FPB.
Pertanyaan 1: Apa perbedaan antara KPK dan FPB?
KPK adalah kelipatan persekutuan terkecil, sedangkan FPB adalah faktor persekutuan terbesar. KPK adalah bilangan terkecil yang habis dibagi oleh kedua bilangan, sedangkan FPB adalah bilangan terbesar yang membagi kedua bilangan tanpa sisa.
Pertanyaan 2: Bagaimana cara menghitung KPK dan FPB?
KPK dapat dihitung dengan mengalikan semua faktor prima yang sama dan berlainan dari kedua bilangan. Sedangkan FPB dapat dihitung dengan mengalikan semua faktor prima yang sama dari kedua bilangan.
Pertanyaan 3: Apa saja aplikasi KPK dan FPB dalam kehidupan sehari-hari?
KPK dan FPB memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti mencari waktu paling singkat yang dibutuhkan agar dua peristiwa terjadi bersamaan, menentukan ukuran terkecil yang dapat dibagi rata oleh beberapa objek, menyederhanakan pecahan, dan menyelesaikan persamaan.
Pertanyaan 4: Mengapa KPK dan FPB penting dalam matematika?
KPK dan FPB adalah konsep dasar dalam matematika yang banyak digunakan dalam berbagai bidang, seperti aljabar, geometri, dan teori bilangan. Pemahaman tentang KPK dan FPB sangat penting untuk menyelesaikan berbagai permasalahan matematika dan kehidupan sehari-hari.
Dengan memahami konsep KPK dan FPB, kita dapat menyelesaikan berbagai masalah matematika dan kehidupan sehari-hari dengan lebih mudah dan efisien.
Lanjutkan membaca untuk mempelajari lebih lanjut tentang aplikasi KPK dan FPB dalam berbagai bidang.
Tips Memahami KPK dan FPB
Kelipatan persekutuan terkecil (KPK) dan faktor persekutuan terbesar (FPB) merupakan konsep dasar dalam matematika yang sangat penting untuk dikuasai. Berikut adalah beberapa tips untuk membantu Anda memahami KPK dan FPB:
Tip 1: Pahami Definisi KPK dan FPB
KPK adalah bilangan terkecil yang habis dibagi oleh dua bilangan atau lebih, sedangkan FPB adalah bilangan terbesar yang membagi dua bilangan atau lebih tanpa sisa.
Tip 2: Gunakan Metode yang Tepat
Ada beberapa metode yang dapat digunakan untuk menghitung KPK dan FPB, seperti metode faktorisasi prima dan metode bagi bersusun. Pilihlah metode yang paling sesuai dengan tingkat kesulitan soal.
Tip 3: Latihan Soal Secara Teratur
Pemahaman tentang KPK dan FPB akan semakin kuat dengan latihan soal secara teratur. Kerjakan berbagai jenis soal untuk mengasah kemampuan Anda.
Tip 4: Pahami Aplikasi KPK dan FPB
KPK dan FPB memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti mencari waktu paling singkat yang dibutuhkan agar dua peristiwa terjadi bersamaan, menentukan ukuran terkecil yang dapat dibagi rata oleh beberapa objek, dan menyederhanakan pecahan.
Tip 5: Hubungkan dengan Konsep Matematika Lainnya
KPK dan FPB terkait dengan konsep matematika lainnya, seperti faktorisasi prima, aljabar, dan geometri. Memahami hubungan ini akan membantu Anda menguasai KPK dan FPB dengan lebih baik.
Kesimpulan:
Dengan memahami tips-tips di atas, Anda dapat meningkatkan pemahaman Anda tentang KPK dan FPB. Konsep ini merupakan dasar penting untuk berbagai bidang matematika, jadi pastikan Anda menguasainya dengan baik.
Youtube Video:










