Luas segitiga siku-siku adalah ukuran besar kecilnya permukaan segitiga yang memiliki satu sudut siku-siku (90 derajat). Rumus untuk menghitung luas segitiga siku-siku adalah setengah dari hasil perkalian panjang alas dan tinggi segitiga. Misalnya, jika alas segitiga siku-siku adalah 10 cm dan tingginya 8 cm, maka luasnya adalah x 10 cm x 8 cm = 40 cm persegi.
Mengetahui luas segitiga siku-siku penting dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Dalam arsitektur, luas segitiga siku-siku digunakan untuk menghitung luas atap atau dinding bangunan. Dalam teknik, luas segitiga siku-siku digunakan untuk menghitung luas bidang pada objek tiga dimensi. Dalam desain, luas segitiga siku-siku digunakan untuk menghitung luas bidang pada logo atau desain lainnya.
Konsep luas segitiga siku-siku sudah dikenal sejak zaman kuno. Matematikawan Yunani Pythagoras mengembangkan teorema terkenal yang dikenal sebagai Teorema Pythagoras, yang menghubungkan panjang sisi-sisi segitiga siku-siku dengan luasnya. Teorema Pythagoras telah banyak digunakan dalam berbagai bidang, termasuk geometri, trigonometri, dan fisika.
Luas Segitiga Siku-Siku
Luas segitiga siku-siku merupakan aspek penting dalam matematika dan memiliki berbagai aplikasi dalam kehidupan sehari-hari. Berikut adalah tujuh aspek penting terkait luas segitiga siku-siku:
- Rumus: 1/2 x alas x tinggi
- Satuan: Satuan luas (cm, m, dll.)
- Sifat: Selalu bernilai positif
- Aplikasi: Menghitung luas atap, luas dinding, dan luas bangun ruang
- Sejarah: Ditemukan oleh Pythagoras
- Teorema Pythagoras: Menghubungkan luas segitiga siku-siku dengan panjang sisi-sisinya
- Trigonometri: Digunakan untuk menghitung luas segitiga siku-siku yang tidak diketahui panjang sisi-sisinya
Ketujuh aspek tersebut saling berkaitan dan membentuk pemahaman yang komprehensif tentang luas segitiga siku-siku. Misalnya, rumus luas segitiga siku-siku digunakan dalam berbagai aplikasi, seperti menghitung luas atap rumah atau luas dinding bangunan. Sifat luas segitiga siku-siku yang selalu bernilai positif menunjukkan bahwa luas segitiga tidak dapat bernilai negatif, yang sesuai dengan konsep luas sebagai ukuran besar kecilnya suatu permukaan. Teorema Pythagoras dan trigonometri memberikan metode alternatif untuk menghitung luas segitiga siku-siku, yang berguna ketika panjang sisi-sisinya tidak diketahui.
Rumus
Rumus 1/2 x alas x tinggi merupakan rumus untuk menghitung luas segitiga siku-siku. Rumus ini sangat penting karena memberikan cara yang mudah dan akurat untuk menghitung luas segitiga siku-siku, yang memiliki banyak aplikasi dalam kehidupan sehari-hari.
Rumus ini diturunkan dari sifat-sifat segitiga siku-siku. Segitiga siku-siku memiliki satu sudut siku-siku (90 derajat), dan panjang sisi-sisinya yang saling tegak lurus disebut alas dan tinggi. Luas segitiga siku-siku adalah setengah dari hasil perkalian alas dan tinggi karena bentuk segitiga siku-siku dapat dianggap sebagai setengah dari persegi panjang dengan panjang dan lebar yang sama dengan alas dan tinggi segitiga.
Rumus 1/2 x alas x tinggi sangat penting karena memungkinkan kita untuk menghitung luas segitiga siku-siku meskipun kita tidak mengetahui panjang ketiga sisinya. Hal ini sangat berguna dalam berbagai aplikasi, seperti menghitung luas atap rumah, luas bidang miring pada benda tiga dimensi, dan luas bayangan pada benda yang terkena sinar matahari.
Satuan
Satuan luas sangat penting dalam konteks luas segitiga siku-siku karena memungkinkan kita untuk menyatakan besarnya luas dalam besaran yang terukur dan dapat dibandingkan. Satuan luas yang umum digunakan antara lain sentimeter persegi (cm), meter persegi (m), dan kilometer persegi (km).
-
Pengukuran Luas
Satuan luas digunakan untuk mengukur luas permukaan suatu benda, termasuk luas segitiga siku-siku. Dengan menggunakan satuan luas, kita dapat membandingkan besarnya luas benda yang berbeda dan menentukan benda yang memiliki luas lebih besar atau lebih kecil.
-
Konversi Satuan
Satuan luas dapat dikonversi dari satu satuan ke satuan lainnya sesuai kebutuhan. Misalnya, kita dapat mengonversi sentimeter persegi ke meter persegi dengan membagi dengan 10.000, atau mengonversi meter persegi ke kilometer persegi dengan membagi dengan 1.000.000.
-
Aplikasi Praktis
Satuan luas memiliki banyak aplikasi praktis dalam kehidupan sehari-hari. Misalnya, satuan luas digunakan dalam arsitektur untuk menghitung luas lantai dan dinding bangunan, dalam pertanian untuk menentukan luas lahan pertanian, dan dalam teknik untuk menghitung luas permukaan benda.
-
Standarisasi
Penggunaan satuan luas yang standar memastikan konsistensi dan akurasi dalam pengukuran luas. Hal ini penting untuk berbagai tujuan, seperti perencanaan pembangunan, penentuan pajak properti, dan perbandingan hasil pengukuran yang dilakukan oleh orang yang berbeda.
Dengan memahami satuan luas dan penggunaannya dalam konteks luas segitiga siku-siku, kita dapat mengukur, membandingkan, dan menyatakan luas permukaan benda dengan jelas dan akurat.
Sifat
Salah satu sifat dari luas segitiga siku-siku adalah selalu bernilai positif. Sifat ini sangat penting karena memiliki implikasi yang signifikan dalam berbagai aspek.
Pertama, sifat ini menunjukkan bahwa luas segitiga siku-siku tidak dapat bernilai negatif. Hal ini masuk akal secara intuitif karena luas merupakan ukuran besar kecilnya suatu permukaan, dan tidak mungkin suatu permukaan memiliki luas negatif. Sifat ini memastikan bahwa luas segitiga siku-siku selalu menunjukkan besarnya permukaan yang sebenarnya.
Kedua, sifat ini menyederhanakan banyak perhitungan yang melibatkan luas segitiga siku-siku. Misalnya, ketika menghitung luas total suatu bangun datar yang terdiri dari beberapa segitiga siku-siku, kita dapat langsung menjumlahkan luas masing-masing segitiga tanpa perlu khawatir tentang tanda negatif. Sifat ini membuat proses perhitungan menjadi lebih mudah dan efisien.
Ketiga, sifat ini memiliki implikasi penting dalam aplikasi praktis. Misalnya, dalam arsitektur, luas segitiga siku-siku digunakan untuk menghitung luas atap bangunan. Sifat positif dari luas segitiga siku-siku memastikan bahwa luas atap selalu bernilai positif, yang penting untuk memastikan bahwa atap dapat menahan beban dan melindungi bangunan dari cuaca.
Aplikasi
Salah satu aplikasi penting dari luas segitiga siku-siku adalah untuk menghitung luas atap, luas dinding, dan luas bangun ruang. Hal ini karena banyak atap dan dinding bangunan memiliki bentuk segitiga siku-siku, dan luas bangun ruang dapat dihitung dengan menjumlahkan luas permukaan sisi-sisinya yang berbentuk segitiga siku-siku.
Dalam arsitektur, menghitung luas atap dan luas dinding sangat penting untuk menentukan jumlah bahan bangunan yang dibutuhkan, seperti genteng, panel dinding, dan cat. Dengan mengetahui luas permukaan bangunan, arsitek dapat memperkirakan biaya pembangunan dan memastikan bahwa bangunan memiliki luas yang cukup untuk memenuhi kebutuhan penghuninya.
Selain dalam arsitektur, luas segitiga siku-siku juga digunakan untuk menghitung luas permukaan benda tiga dimensi, seperti prisma, limas, dan kerucut. Dengan menjumlahkan luas permukaan sisi-sisinya yang berbentuk segitiga siku-siku, kita dapat menentukan luas permukaan total benda tersebut. Hal ini penting untuk berbagai tujuan, seperti menghitung luas permukaan benda yang akan dicat atau dilapisi bahan tertentu.
Sejarah
Hubungan antara sejarah penemuan luas segitiga siku-siku dengan konsep luas segitiga siku-siku itu sendiri sangatlah penting. Penemuan ini menjadi dasar pemahaman kita tentang sifat-sifat dan aplikasi luas segitiga siku-siku.
-
Teorema Pythagoras
Penemuan Pythagoras yang paling terkenal adalah Teorema Pythagoras, yang menyatakan bahwa kuadrat panjang sisi miring pada segitiga siku-siku sama dengan jumlah kuadrat panjang sisi lainnya. Teorema ini memberikan dasar matematis untuk menghitung luas segitiga siku-siku, karena luas segitiga siku-siku dapat dihitung sebagai setengah dari hasil kali panjang sisi alas dan tinggi, yang keduanya dapat dihitung menggunakan Teorema Pythagoras.
-
Pembuktian Geometris
Pythagoras juga memberikan pembuktian geometris untuk rumus luas segitiga siku-siku. Pembuktian ini didasarkan pada penguraian segitiga siku-siku menjadi dua segitiga siku-siku yang lebih kecil, yang masing-masing memiliki alas dan tinggi setengah dari alas dan tinggi segitiga siku-siku asli. Dengan menghitung luas kedua segitiga siku-siku yang lebih kecil dan menjumlahkannya, Pythagoras menunjukkan bahwa luas segitiga siku-siku asli sama dengan setengah dari hasil kali panjang alas dan tinggi.
-
Aplikasi Praktis
Penemuan luas segitiga siku-siku oleh Pythagoras memiliki banyak aplikasi praktis dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Misalnya, dalam arsitektur, rumus luas segitiga siku-siku digunakan untuk menghitung luas atap dan dinding bangunan. Dalam teknik, rumus ini digunakan untuk menghitung luas permukaan benda tiga dimensi, seperti prisma dan limas.
Ketiga aspek ini menunjukkan bahwa penemuan luas segitiga siku-siku oleh Pythagoras adalah tonggak penting dalam pengembangan matematika dan memiliki dampak yang luas pada aplikasi praktisnya.
Teorema Pythagoras
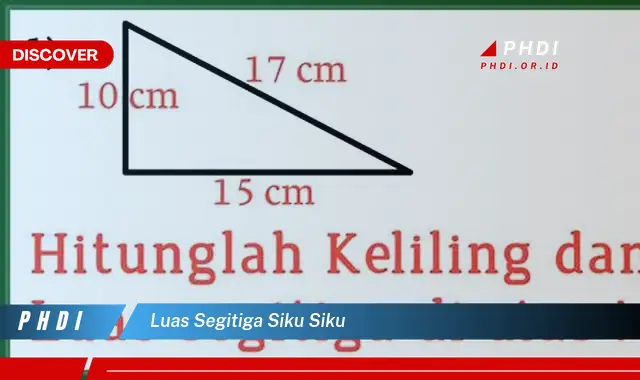
Teorema Pythagoras merupakan teorema penting dalam geometri yang menghubungkan panjang sisi-sisi segitiga siku-siku dengan luasnya. Teorema ini menyatakan bahwa kuadrat panjang sisi miring pada segitiga siku-siku sama dengan jumlah kuadrat panjang sisi lainnya. Dengan kata lain, jika a, b, dan c masing-masing adalah panjang sisi alas, tinggi, dan sisi miring segitiga siku-siku, maka berlaku:$$a^2 + b^2 = c^2$$Persamaan ini memiliki implikasi penting terhadap luas segitiga siku-siku. Luas segitiga siku-siku dapat dihitung sebagai setengah dari hasil kali panjang alas dan tinggi. Dengan menggunakan Teorema Pythagoras, kita dapat menyatakan alas dan tinggi segitiga siku-siku dalam kaitannya dengan sisi miring.Misalkan kita memiliki segitiga siku-siku dengan sisi miring c dan alas a. Dengan menggunakan Teorema Pythagoras, kita dapat mencari tinggi b sebagai berikut:$$b^2 = c^2 – a^2$$$$b = \sqrt{c^2 – a^2}$$Dengan mensubstitusikan persamaan ini ke dalam rumus luas segitiga siku-siku, kita memperoleh:$$Luas = \frac{1}{2} \times a \times \sqrt{c^2 – a^2}$$Persamaan ini menunjukkan bahwa luas segitiga siku-siku dapat dihitung jika kita mengetahui panjang sisi alas dan sisi miringnya. Teorema Pythagoras menyediakan hubungan penting antara luas segitiga siku-siku dan panjang sisi-sisinya, menjadikannya teorema penting dalam geometri dan memiliki banyak aplikasi dalam berbagai bidang.
Trigonometri
Trigonometri merupakan cabang matematika yang mempelajari hubungan antara sisi-sisi dan sudut-sudut segitiga. Salah satu aplikasi penting trigonometri adalah untuk menghitung luas segitiga siku-siku yang tidak diketahui panjang sisi-sisinya.
-
Menggunakan Fungsi Sinus dan Kosinus
Dalam segitiga siku-siku, fungsi sinus dan kosinus dapat digunakan untuk mencari panjang sisi yang tidak diketahui jika kita mengetahui sudut dan satu sisi lainnya. Misalnya, jika kita mengetahui panjang alas segitiga siku-siku dan sudut yang berhadapan dengan alas tersebut, kita dapat menggunakan fungsi sinus untuk mencari tinggi segitiga. Dengan mengetahui panjang alas dan tinggi, kita dapat menghitung luas segitiga menggunakan rumus yang telah dijelaskan sebelumnya.
-
Menggunakan Fungsi Tangent
Fungsi tangen dapat digunakan untuk mencari panjang sisi yang tidak diketahui jika kita mengetahui dua sudut lainnya. Misalnya, jika kita mengetahui sudut-sudut yang berhadapan dengan sisi alas dan sisi tinggi, kita dapat menggunakan fungsi tangen untuk mencari panjang salah satu sisi tersebut. Dengan mengetahui panjang sisi alas dan tinggi, kita dapat menghitung luas segitiga.
-
Aplikasi Praktis
Kemampuan trigonometri untuk menghitung luas segitiga siku-siku yang tidak diketahui panjang sisi-sisinya memiliki banyak aplikasi praktis. Misalnya, trigonometri digunakan dalam survei tanah untuk menentukan luas bidang tanah, dalam arsitektur untuk menghitung luas atap bangunan, dan dalam navigasi untuk menentukan posisi kapal atau pesawat.
Dengan demikian, trigonometri merupakan alat yang ampuh untuk menghitung luas segitiga siku-siku, bahkan ketika panjang sisi-sisinya tidak diketahui. Aplikasi trigonometri ini memiliki peran penting dalam berbagai bidang, seperti survei tanah, arsitektur, dan navigasi.
Pertanyaan Umum tentang Luas Segitiga Siku-Siku
Bagian ini akan menjawab beberapa pertanyaan umum tentang luas segitiga siku-siku untuk memberikan pemahaman yang lebih mendalam.
Pertanyaan 1: Bagaimana cara menghitung luas segitiga siku-siku?
Luas segitiga siku-siku dapat dihitung dengan menggunakan rumus: 1/2 x alas x tinggi, di mana alas adalah sisi yang mendatar dan tinggi adalah sisi yang tegak lurus terhadap alas.
Pertanyaan 2: Apa saja aplikasi praktis dari menghitung luas segitiga siku-siku?
Menghitung luas segitiga siku-siku memiliki berbagai aplikasi praktis, antara lain dalam arsitektur (menghitung luas atap dan dinding), teknik (menghitung luas permukaan benda), dan desain (menghitung luas bidang pada logo atau desain lainnya).
Pertanyaan 3: Bagaimana cara menghitung luas segitiga siku-siku jika tidak diketahui panjang sisi-sisinya?
Untuk menghitung luas segitiga siku-siku jika tidak diketahui panjang sisi-sisinya, dapat digunakan trigonometri. Fungsi sinus, kosinus, dan tangen dapat digunakan untuk mencari panjang sisi yang tidak diketahui jika diketahui sudut dan satu sisi lainnya.
Pertanyaan 4: Mengapa penting untuk memahami luas segitiga siku-siku?
Memahami luas segitiga siku-siku penting karena banyak aplikasi praktisnya dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Selain itu, konsep luas segitiga siku-siku merupakan dasar untuk memahami konsep luas bangun datar lainnya.
Dengan memahami jawaban dari pertanyaan umum ini, diharapkan pemahaman tentang luas segitiga siku-siku semakin komprehensif.
Kembali ke artikel utama tentang Luas Segitiga Siku-Siku.
Tips Mengitung Luas Segitiga Siku-siku
Mengitung luas segitiga siku-siku merupakan keterampilan dasar dalam geometri dengan berbagai aplikasi praktis. Berikut adalah beberapa tips untuk membantu Anda menghitung luas segitiga siku-siku secara akurat dan efisien:
Tip 1: Pastikan Anda Memiliki Rumus yang Benar
Rumus untuk menghitung luas segitiga siku-siku adalah 1/2 x alas x tinggi.
Tip 2: Identifikasi Alas dan Tinggi
Alas adalah sisi yang mendatar, sedangkan tinggi adalah sisi yang tegak lurus terhadap alas.
Tip 3: Periksa Satuan
Pastikan satuan yang digunakan untuk panjang alas dan tinggi sama, biasanya sentimeter atau meter.
Tip 4: Gunakan Kalkulator atau Gambar
Jika diperlukan, gunakan kalkulator atau buat gambar segitiga siku-siku untuk membantu menghitung luasnya.
Tip 5: Periksa Hasil Anda
Setelah menghitung luas, periksa kembali hasil Anda dengan mengukur ulang alas dan tinggi atau menggunakan metode lain.
Dengan mengikuti tips ini, Anda dapat menghitung luas segitiga siku-siku dengan percaya diri dan akurat. Keterampilan ini akan berguna dalam berbagai bidang, termasuk arsitektur, teknik, dan desain.
Kembali ke artikel utama tentang Luas Segitiga Siku-Siku.
Youtube Video:










