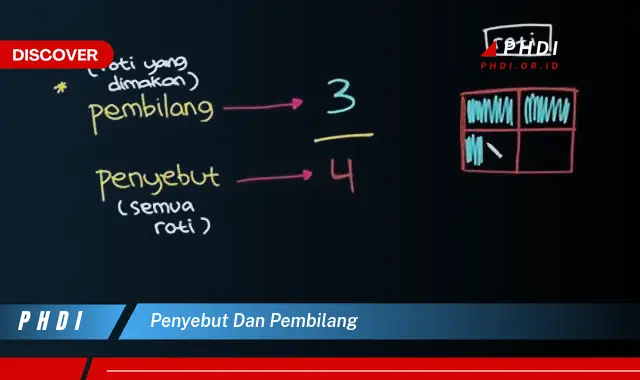
Dalam matematika, penyebut dan pembilang adalah dua bilangan yang membentuk pecahan. Penyebut adalah bilangan di bagian bawah pecahan, yang menunjukkan banyaknya bagian yang sama dalam keseluruhan. Pembilang adalah bilangan di bagian atas pecahan, yang menunjukkan banyaknya bagian yang diambil dari keseluruhan.
Penyebut dan pembilang sangat penting dalam matematika karena memungkinkan kita untuk mewakili bagian-bagian dari suatu keseluruhan dan membandingkan besaran yang berbeda. Misalnya, pecahan 1/2 mewakili setengah dari keseluruhan, sedangkan pecahan 3/4 mewakili tiga perempat dari keseluruhan. Dengan membandingkan penyebut dan pembilang pecahan, kita dapat dengan mudah menentukan pecahan mana yang lebih besar atau lebih kecil.
Konsep penyebut dan pembilang telah digunakan selama berabad-abad dalam berbagai budaya. Pecahan pertama kali digunakan oleh bangsa Babilonia pada sekitar tahun 2000 SM. Bangsa Mesir kemudian mengembangkan sistem pecahan mereka sendiri, yang menggunakan hieroglif untuk mewakili pecahan yang berbeda. Sistem pecahan modern yang kita gunakan saat ini dikembangkan pada abad ke-16 oleh matematikawan Prancis Franois Vite.
Penyebut dan Pembilang
Penyebut dan pembilang adalah dua bilangan yang sangat penting dalam matematika. Keduanya digunakan untuk membentuk pecahan, yang merupakan cara untuk menyatakan bagian dari suatu keseluruhan. Penyebut terletak di bagian bawah pecahan dan menunjukkan banyaknya bagian yang sama dalam keseluruhan. Pembilang terletak di bagian atas pecahan dan menunjukkan banyaknya bagian yang diambil dari keseluruhan.
- Bagian dari keseluruhan
- Membandingkan besaran
- Operasi hitung pecahan
- Geometri
- Probabilitas
- Statistika
- Aplikasi kehidupan nyata
Ketujuh aspek ini saling terkait dan membentuk dasar untuk memahami dan menggunakan pecahan dalam berbagai bidang matematika dan kehidupan nyata. Misalnya, dalam geometri, pecahan dapat digunakan untuk menyatakan panjang sisi segitiga atau jari-jari lingkaran. Dalam probabilitas, pecahan dapat digunakan untuk menyatakan peluang suatu kejadian. Dan dalam statistika, pecahan dapat digunakan untuk menyatakan rata-rata atau median suatu kumpulan data. Dengan memahami konsep penyebut dan pembilang, kita dapat menggunakan pecahan untuk menyelesaikan masalah dan membuat keputusan yang lebih baik dalam berbagai bidang kehidupan.
Bagian dari keseluruhan
Konsep bagian dari keseluruhan sangat penting dalam matematika, dan penyebut dan pembilang memainkan peran penting dalam menyatakan bagian-bagian ini. Penyebut menunjukkan banyaknya bagian yang sama dalam keseluruhan, sedangkan pembilang menunjukkan banyaknya bagian yang diambil dari keseluruhan.
-
Ukuran dan pembagian
Penyebut dan pembilang dapat digunakan untuk menyatakan ukuran bagian dari keseluruhan. Misalnya, pecahan 1/2 menyatakan setengah dari keseluruhan, sedangkan pecahan 3/4 menyatakan tiga perempat dari keseluruhan. Pecahan juga dapat digunakan untuk menyatakan pembagian suatu keseluruhan menjadi bagian-bagian yang sama. Misalnya, jika kita membagi sebuah pizza menjadi 8 bagian yang sama, setiap bagian dapat dinyatakan sebagai 1/8 dari keseluruhan pizza.
-
Proporsi dan persentase
Penyebut dan pembilang juga dapat digunakan untuk menyatakan proporsi dan persentase. Proporsi adalah perbandingan dua bilangan, sedangkan persentase adalah proporsi yang dinyatakan dalam per seratus. Misalnya, jika kita memiliki sebuah kelas dengan 20 siswa dan 12 siswa di antaranya adalah perempuan, maka proporsi siswa perempuan dalam kelas tersebut adalah 12/20 atau 60%.
-
Probabilitas
Dalam probabilitas, penyebut dan pembilang digunakan untuk menyatakan peluang suatu kejadian. Peluang suatu kejadian adalah ukuran seberapa besar kemungkinan kejadian tersebut terjadi. Peluang dinyatakan sebagai pecahan, dengan penyebut sebagai jumlah semua kemungkinan hasil dan pembilang sebagai jumlah hasil yang diinginkan.
-
Statistika
Dalam statistika, penyebut dan pembilang digunakan untuk menyatakan rata-rata dan median suatu kumpulan data. Rata-rata adalah jumlah semua data dibagi dengan jumlah data, sedangkan median adalah nilai tengah dari suatu kumpulan data. Rata-rata dan median dapat dinyatakan sebagai pecahan, dengan penyebut sebagai jumlah data dan pembilang sebagai jumlah data yang dijumlahkan atau nilai tengah.
Dengan memahami konsep penyebut dan pembilang, kita dapat menyatakan dan menghitung bagian-bagian dari keseluruhan dalam berbagai bidang matematika dan kehidupan nyata.
Membandingkan Besaran
Membandingkan besaran adalah salah satu konsep dasar dalam matematika, dan penyebut dan pembilang memainkan peran penting dalam proses ini. Penyebut dan pembilang memungkinkan kita untuk membandingkan besaran yang berbeda dengan cara yang terstruktur dan sistematis.
-
Ukuran dan satuan
Penyebut dan pembilang dapat digunakan untuk membandingkan ukuran yang berbeda dengan satuan yang sama. Misalnya, jika kita memiliki dua wadah yang berisi air, kita dapat membandingkan jumlah air di setiap wadah dengan membandingkan penyebut pecahan yang menyatakan jumlah air di setiap wadah. Wadah dengan penyebut lebih besar berisi lebih banyak air.
-
Nilai pecahan
Penyebut dan pembilang juga dapat digunakan untuk membandingkan nilai pecahan yang berbeda. Pecahan dengan penyebut yang sama, pecahan dengan pembilang yang lebih besar memiliki nilai yang lebih besar. Misalnya, pecahan 3/4 lebih besar dari pecahan 2/4 karena pembilangnya lebih besar.
-
Proporsi dan persentase
Penyebut dan pembilang juga dapat digunakan untuk membandingkan proporsi dan persentase yang berbeda. Proporsi dengan penyebut yang sama, proporsi dengan pembilang yang lebih besar memiliki nilai yang lebih besar. Misalnya, proporsi 3:4 lebih besar dari proporsi 2:4 karena pembilangnya lebih besar.
-
Skala dan grafik
Penyebut dan pembilang juga dapat digunakan untuk membandingkan skala dan grafik yang berbeda. Skala atau grafik dengan penyebut yang sama, skala atau grafik dengan pembilang yang lebih besar memiliki nilai yang lebih besar. Misalnya, skala 1:100 lebih besar dari skala 1:200 karena pembilangnya lebih besar.
Dengan memahami konsep penyebut dan pembilang, kita dapat membandingkan besaran yang berbeda dengan mudah dan akurat. Konsep ini sangat penting dalam berbagai bidang matematika dan kehidupan nyata, seperti sains, teknik, ekonomi, dan keuangan.
Operasi Hitung Pecahan
Operasi hitung pecahan merupakan operasi matematika yang dilakukan pada bilangan pecahan. Operasi hitung pecahan meliputi penjumlahan, pengurangan, perkalian, dan pembagian pecahan. Dalam operasi hitung pecahan, penyebut dan pembilang berperan sangat penting dalam menentukan hasil operasi.
-
Penjumlahan dan Pengurangan Pecahan
Dalam penjumlahan dan pengurangan pecahan, penyebut pecahan harus disamakan terlebih dahulu. Penyebut yang disamakan disebut dengan kelipatan persekutuan terkecil (KPK). Setelah penyebut disamakan, operasi penjumlahan atau pengurangan dapat dilakukan pada pembilang pecahan.
-
Perkalian Pecahan
Dalam perkalian pecahan, penyebut pecahan pertama dikalikan dengan penyebut pecahan kedua, dan pembilang pecahan pertama dikalikan dengan pembilang pecahan kedua. Hasil perkalian penyebut menjadi penyebut pecahan hasil kali, dan hasil perkalian pembilang menjadi pembilang pecahan hasil kali.
-
Pembagian Pecahan
Dalam pembagian pecahan, pecahan pertama dibalik (pembilang menjadi penyebut, dan penyebut menjadi pembilang), kemudian dikalikan dengan pecahan kedua. Hasil perkalian penyebut menjadi penyebut pecahan hasil bagi, dan hasil perkalian pembilang menjadi pembilang pecahan hasil bagi.
Operasi hitung pecahan sangat penting dalam matematika karena memungkinkan kita untuk melakukan berbagai perhitungan yang melibatkan pecahan. Konsep penyebut dan pembilang sangat penting dalam operasi hitung pecahan, karena keduanya menentukan hasil operasi.
Geometri
Dalam geometri, penyebut dan pembilang memainkan peran penting dalam menyatakan besaran dan hubungan antara bangun geometri. Penyebut dan pembilang dapat digunakan untuk menyatakan panjang sisi, luas, dan volume bangun geometri, serta untuk menyatakan skala dan transformasi geometri.
-
Ukuran dan Bentuk Bangun Geometri
Penyebut dan pembilang dapat digunakan untuk menyatakan panjang sisi, luas, dan volume bangun geometri. Misalnya, panjang sisi sebuah persegi panjang dapat dinyatakan sebagai penyebut dari pecahan yang menyatakan luas persegi panjang tersebut. Demikian pula, volume sebuah kubus dapat dinyatakan sebagai penyebut dari pecahan yang menyatakan luas permukaan kubus tersebut.
-
Skala dan Transformasi Geometri
Penyebut dan pembilang juga dapat digunakan untuk menyatakan skala dan transformasi geometri. Misalnya, skala sebuah gambar dapat dinyatakan sebagai pecahan yang menyatakan perbandingan panjang sisi gambar tersebut dengan panjang sisi objek sebenarnya. Demikian pula, transformasi geometri seperti translasi, rotasi, dan dilatasi dapat dinyatakan menggunakan pecahan yang menyatakan pergeseran, sudut rotasi, atau faktor skala.
Dengan memahami konsep penyebut dan pembilang, kita dapat menyatakan dan menghitung besaran dan hubungan antara bangun geometri dengan mudah dan akurat. Konsep ini sangat penting dalam berbagai bidang matematika dan kehidupan nyata, seperti arsitektur, teknik sipil, desain grafis, dan animasi.
Probabilitas
Probabilitas adalah ukuran seberapa besar kemungkinan suatu kejadian terjadi. Probabilitas dinyatakan sebagai pecahan, dengan penyebut sebagai jumlah semua kemungkinan hasil dan pembilang sebagai jumlah hasil yang diinginkan.
-
Ruang Sampel
Ruang sampel adalah himpunan semua kemungkinan hasil suatu percobaan. Penyebut dari suatu probabilitas adalah jumlah anggota ruang sampel.
-
Kejadian
Kejadian adalah himpunan bagian dari ruang sampel. Pembilang dari suatu probabilitas adalah jumlah anggota kejadian.
-
Peluang Empiris
Peluang empiris adalah peluang suatu kejadian yang diperkirakan berdasarkan pengamatan atau eksperimen. Peluang empiris dapat dihitung dengan membagi jumlah kejadian yang diamati dengan jumlah percobaan.
-
Peluang Teoretis
Peluang teoretis adalah peluang suatu kejadian yang dihitung berdasarkan teori probabilitas. Peluang teoretis dapat dihitung dengan membagi jumlah hasil yang diinginkan dengan jumlah semua kemungkinan hasil.
Konsep penyebut dan pembilang sangat penting dalam probabilitas karena memungkinkan kita untuk menyatakan dan menghitung peluang suatu kejadian dengan jelas dan akurat. Konsep ini sangat penting dalam berbagai bidang matematika dan kehidupan nyata, seperti statistika, ilmu komputer, dan kecerdasan buatan.
Statistika
Statistika adalah ilmu yang mempelajari tentang pengumpulan, pengolahan, analisis, dan penafsiran data. Penyebut dan pembilang memainkan peran penting dalam statistika, karena keduanya digunakan untuk menyatakan dan menghitung ukuran-ukuran statistik yang penting.
Salah satu ukuran statistik yang penting adalah rata-rata. Rata-rata adalah jumlah semua data dibagi dengan jumlah data. Rata-rata dapat dinyatakan sebagai pecahan, dengan penyebut sebagai jumlah data dan pembilang sebagai jumlah semua data.
Ukuran statistik penting lainnya adalah median. Median adalah nilai tengah dari suatu kumpulan data. Median juga dapat dinyatakan sebagai pecahan, dengan penyebut sebagai jumlah data dan pembilang sebagai nilai tengah.
Selain rata-rata dan median, penyebut dan pembilang juga digunakan untuk menghitung ukuran statistik lainnya, seperti varians, standar deviasi, dan koefisien korelasi. Ukuran-ukuran statistik ini sangat penting dalam statistika, karena memungkinkan kita untuk mendeskripsikan dan menganalisis data dengan lebih baik.
Dengan memahami konsep penyebut dan pembilang, kita dapat menggunakan statistika untuk memecahkan masalah dan membuat keputusan yang lebih baik dalam berbagai bidang kehidupan.
Aplikasi Kehidupan Nyata
Konsep penyebut dan pembilang memiliki banyak aplikasi dalam kehidupan nyata di berbagai bidang, antara lain:
-
Matematika keuangan
Penyebut dan pembilang digunakan untuk menghitung bunga, cicilan, dan nilai investasi. -
Fisika
Penyebut dan pembilang digunakan untuk menyatakan besaran fisika, seperti kecepatan, percepatan, dan gaya. -
Teknik
Penyebut dan pembilang digunakan untuk menghitung beban, tegangan, dan momen gaya. -
Kedokteran
Penyebut dan pembilang digunakan untuk menyatakan dosis obat, konsentrasi larutan, dan hasil pemeriksaan laboratorium. -
Ekonomi
Penyebut dan pembilang digunakan untuk menghitung inflasi, tingkat pengangguran, dan pertumbuhan ekonomi.
Dengan memahami konsep penyebut dan pembilang, kita dapat menggunakannya untuk memecahkan masalah dan membuat keputusan yang lebih baik dalam berbagai aspek kehidupan nyata.
Pertanyaan Umum tentang Penyebut dan Pembilang
Berikut adalah beberapa pertanyaan umum tentang penyebut dan pembilang, beserta jawabannya.
Pertanyaan 1: Apa yang dimaksud dengan penyebut dan pembilang?
Penyebut adalah bilangan di bagian bawah pecahan yang menunjukkan banyaknya bagian yang sama dalam keseluruhan. Pembilang adalah bilangan di bagian atas pecahan yang menunjukkan banyaknya bagian yang diambil dari keseluruhan.
Pertanyaan 2: Bagaimana cara menyederhanakan pecahan?
Untuk menyederhanakan pecahan, kita dapat membagi penyebut dan pembilang dengan faktor persekutuan terbesar (FPB) dari keduanya.
Pertanyaan 3: Bagaimana cara menjumlahkan atau mengurangkan pecahan?
Untuk menjumlahkan atau mengurangkan pecahan, kita harus terlebih dahulu menyetarakan penyebutnya. Setelah penyebutnya sama, kita dapat menjumlahkan atau mengurangkan pembilangnya.
Pertanyaan 4: Bagaimana cara mengalikan atau membagi pecahan?
Untuk mengalikan pecahan, kita kalikan penyebut dengan penyebut dan pembilang dengan pembilang. Untuk membagi pecahan, kita balik pecahan kedua dan kemudian kalikan dengan pecahan pertama.
Dengan memahami konsep penyebut dan pembilang, kita dapat menyelesaikan berbagai operasi hitung pecahan dengan mudah dan akurat.
Transisi ke bagian artikel berikutnya…
Tips Memahami Penyebut dan Pembilang
Konsep penyebut dan pembilang sangat penting dalam matematika, namun terkadang bisa jadi membingungkan. Berikut adalah beberapa tips untuk membantu Anda memahami dan menggunakan penyebut dan pembilang dengan lebih baik:
Tip 1: Pikirkan penyebut sebagai penyebut “kue”. Penyebut menunjukkan berapa banyak bagian yang sama yang membentuk keseluruhan. Misalnya, dalam pecahan 1/2, penyebut 2 menunjukkan bahwa keseluruhan dibagi menjadi dua bagian yang sama.
Tip 2: Pikirkan pembilang sebagai jumlah “potongan kue” yang Anda ambil. Pembilang menunjukkan berapa banyak bagian dari keseluruhan yang Anda ambil. Misalnya, dalam pecahan 1/2, pembilang 1 menunjukkan bahwa Anda mengambil satu bagian dari dua bagian yang sama.
Tip 3: Ingat bahwa penyebut dan pembilang harus selalu ditulis sebagai bilangan bulat. Penyebut tidak boleh negatif, dan pembilang tidak boleh lebih besar dari penyebut.
Tip 4: Gunakan penyederhanaan untuk membuat pecahan lebih sederhana dan mudah dipahami. Penyederhanaan dilakukan dengan membagi penyebut dan pembilang dengan faktor persekutuan terbesar (FPB) dari keduanya.
Tip 5: Gunakan penyebut yang sama saat menjumlahkan atau mengurangkan pecahan. Untuk menjumlahkan atau mengurangkan pecahan, Anda harus terlebih dahulu menyetarakan penyebutnya. Setelah penyebutnya sama, Anda dapat menjumlahkan atau mengurangkan pembilangnya.
Dengan mengikuti tips ini, Anda dapat meningkatkan pemahaman Anda tentang penyebut dan pembilang, dan menggunakannya dengan lebih percaya diri dalam menyelesaikan masalah matematika.
Kesimpulan…
Youtube Video:










