Faktor Persekutuan Terbesar (FPB) dan Kelipatan Persekutuan Terkecil (KPK) merupakan dua konsep penting dalam matematika, khususnya pada topik bilangan bulat.
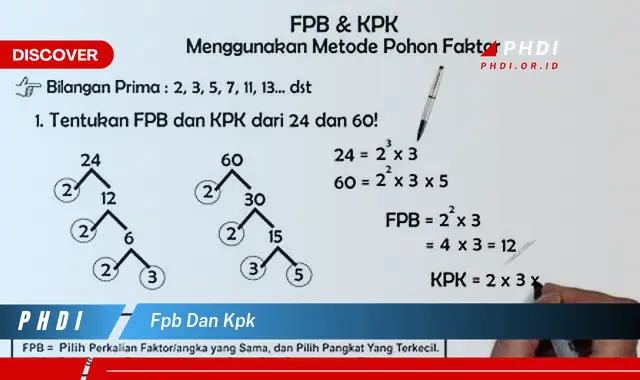
FPB dari dua atau lebih bilangan bulat adalah bilangan bulat terbesar yang membagi semua bilangan tersebut tanpa sisa. Sedangkan KPK dari dua atau lebih bilangan bulat adalah bilangan bulat terkecil yang habis dibagi oleh semua bilangan tersebut. Misalnya, FPB dari 12 dan 18 adalah 6, sedangkan KPK dari 12 dan 18 adalah 36.
FPB dan KPK memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti pada saat mencari satuan terkecil yang dapat digunakan sebagai wadah untuk mengisi beberapa benda atau mencari waktu bersama terpendek yang memungkinkan beberapa orang untuk bertemu. Selain itu, FPB dan KPK juga berperan penting dalam pengembangan algoritma dan teori matematika.
FPB dan KPK
FPB dan KPK merupakan konsep penting dalam matematika, khususnya topik bilangan bulat. Berikut adalah tujuh aspek penting terkait FPB dan KPK:
- Definisi dan sifat
- Algoritma pencarian FPB dan KPK
- Aplikasi dalam kehidupan sehari-hari
- Relasi dengan konsep matematika lainnya
- Sejarah dan perkembangan
- Penerapan dalam bidang studi lain
- Tantangan dan keterbatasan
FPB dan KPK memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti pada saat mencari satuan terkecil yang dapat digunakan sebagai wadah untuk mengisi beberapa benda atau mencari waktu bersama terpendek yang memungkinkan beberapa orang untuk bertemu. Selain itu, FPB dan KPK juga berperan penting dalam pengembangan algoritma dan teori matematika. Memahami aspek-aspek penting FPB dan KPK sangat bermanfaat untuk menguasai konsep matematika secara mendalam.
Definisi dan sifat
Definisi dan sifat FPB dan KPK merupakan aspek penting untuk memahami konsep dasar kedua topik tersebut. Definisi FPB adalah bilangan bulat terbesar yang membagi dua atau lebih bilangan bulat tanpa sisa, sedangkan definisi KPK adalah bilangan bulat terkecil yang habis dibagi oleh dua atau lebih bilangan bulat. Sifat-sifat FPB dan KPK meliputi:
-
Sifat Kelipatan
FPB dari dua atau lebih bilangan merupakan faktor dari setiap kelipatan persekutuan dari bilangan-bilangan tersebut. -
Sifat Pembagi
KPK dari dua atau lebih bilangan merupakan kelipatan dari setiap faktor persekutuan dari bilangan-bilangan tersebut. -
Sifat Keunikan
FPB dan KPK dari dua atau lebih bilangan adalah unik, artinya hanya ada satu FPB dan satu KPK untuk bilangan-bilangan tersebut. -
Sifat Perkalian
FPB dan KPK dari dua atau lebih bilangan dapat dihitung menggunakan operasi perkalian dan pembagian.
Memahami definisi dan sifat FPB dan KPK sangat penting untuk menguasai konsep matematika secara mendalam, karena kedua topik ini menjadi dasar bagi banyak operasi matematika lainnya.
Algoritma pencarian FPB dan KPK
Algoritma pencarian FPB dan KPK merupakan metode sistematis untuk mencari nilai FPB dan KPK dari dua atau lebih bilangan bulat. Algoritma ini sangat penting karena menjadi dasar bagi banyak operasi matematika lainnya. Ada beberapa algoritma pencarian FPB dan KPK yang umum digunakan, salah satunya adalah algoritma Euklidean.
Algoritma Euklidean bekerja dengan cara berulang kali membagi bilangan yang lebih besar dengan bilangan yang lebih kecil, dan mengambil sisa pembagian sebagai bilangan baru yang lebih kecil. Proses ini diulangi hingga sisa pembagian menjadi 0. Bilangan terakhir yang bukan 0 sebelum sisa pembagian menjadi 0 merupakan FPB dari bilangan-bilangan awal.
Algoritma pencarian FPB dan KPK memiliki peran penting dalam operasi matematika lainnya, seperti penyederhanaan pecahan, mencari faktor persekutuan terbesar dari beberapa bilangan, dan mencari kelipatan persekutuan terkecil dari beberapa bilangan. Memahami algoritma pencarian FPB dan KPK sangat penting untuk menguasai konsep matematika secara mendalam.
Aplikasi dalam kehidupan sehari-hari
Konsep FPB dan KPK memiliki banyak aplikasi dalam kehidupan sehari-hari, di antaranya untuk mencari solusi dari berbagai permasalahan praktis yang melibatkan bilangan bulat. Salah satu contoh penerapan FPB adalah dalam mencari satuan terkecil yang dapat digunakan sebagai wadah untuk mengisi beberapa benda dengan ukuran berbeda. Misalnya, jika kita ingin mengisi tiga wadah dengan kapasitas masing-masing 12 liter, 18 liter, dan 24 liter, maka FPB dari ketiga bilangan tersebut (yaitu 6 liter) dapat digunakan sebagai satuan terkecil untuk mengisi ketiga wadah tersebut tanpa ada sisa.
Contoh lainnya adalah dalam mencari waktu bersama terpendek yang memungkinkan beberapa orang untuk bertemu. Misalnya, jika tiga orang memiliki jadwal pertemuan setiap 12 hari, 18 hari, dan 24 hari, maka KPK dari ketiga bilangan tersebut (yaitu 72 hari) dapat digunakan sebagai waktu bersama terpendek yang memungkinkan ketiga orang tersebut untuk bertemu.
Dengan demikian, konsep FPB dan KPK memiliki peran penting dalam membantu kita menyelesaikan berbagai permasalahan praktis dalam kehidupan sehari-hari yang melibatkan bilangan bulat.
Relasi dengan konsep matematika lainnya
Konsep FPB dan KPK memiliki relasi yang erat dengan berbagai konsep matematika lainnya, antara lain teori bilangan, aljabar, dan geometri. Dalam teori bilangan, FPB dan KPK digunakan untuk mempelajari sifat-sifat bilangan bulat, seperti menentukan apakah dua bilangan relatif prima atau tidak. Dalam aljabar, FPB dan KPK digunakan untuk menyederhanakan ekspresi aljabar dan mencari solusi dari persamaan linear. Dalam geometri, FPB dan KPK digunakan untuk mencari luas dan keliling bangun datar dan bangun ruang.
Sejarah dan perkembangan
Konsep FPB dan KPK sudah dikenal sejak zaman kuno. Para matematikawan Yunani seperti Euclid dan Archimedes telah menggunakan konsep ini dalam karya-karya mereka. Algoritma Euklidean untuk mencari FPB juga telah dikenal sejak zaman Yunani kuno.
-
Penggunaan dalam Teori Bilangan
FPB dan KPK memainkan peran penting dalam perkembangan teori bilangan. Konsep ini digunakan untuk mempelajari sifat-sifat bilangan bulat, seperti menentukan apakah dua bilangan relatif prima atau tidak. -
Aplikasi dalam Aljabar
FPB dan KPK juga digunakan dalam aljabar. Konsep ini digunakan untuk menyederhanakan ekspresi aljabar dan mencari solusi dari persamaan linear. -
Penerapan dalam Geometri
FPB dan KPK juga memiliki aplikasi dalam geometri. Konsep ini digunakan untuk mencari luas dan keliling bangun datar dan bangun ruang. -
Perkembangan Modern
Pada abad ke-19, matematikawan seperti Gauss dan Dirichlet mengembangkan teori bilangan lebih lanjut, termasuk konsep FPB dan KPK. Teori-teori ini kemudian menjadi dasar bagi perkembangan matematika modern.
Konsep FPB dan KPK terus berkembang dan digunakan dalam berbagai bidang matematika hingga saat ini. Konsep ini merupakan salah satu dasar penting dalam matematika dan memiliki banyak aplikasi dalam berbagai bidang kehidupan.
Penerapan dalam bidang studi lain
Konsep FPB dan KPK tidak hanya terbatas pada matematika, tetapi juga memiliki aplikasi yang luas dalam berbagai bidang studi lainnya. Salah satu bidang yang banyak memanfaatkan FPB dan KPK adalah fisika, khususnya dalam mekanika. Dalam mekanika, FPB dan KPK digunakan untuk menghitung resultan gaya dan momen gaya yang bekerja pada suatu benda.
Selain fisika, FPB dan KPK juga digunakan dalam kimia, biologi, dan ekonomi. Dalam kimia, FPB dan KPK digunakan untuk menghitung perbandingan mol zat-zat yang bereaksi dalam suatu reaksi kimia. Dalam biologi, FPB dan KPK digunakan untuk menentukan periode bersama dari beberapa organisme yang berinteraksi. Dalam ekonomi, FPB dan KPK digunakan untuk mencari satuan mata uang terkecil yang dapat digunakan untuk membagi sejumlah uang tertentu tanpa sisa.
Penerapan FPB dan KPK dalam berbagai bidang studi lain menunjukkan pentingnya konsep ini sebagai dasar matematika yang fundamental. Dengan memahami FPB dan KPK, kita dapat menyelesaikan berbagai permasalahan praktis di berbagai bidang ilmu pengetahuan.
Tantangan dan keterbatasan
Dalam konteks FPB dan KPK, terdapat beberapa tantangan dan keterbatasan yang perlu dipertimbangkan. Salah satu tantangan utama adalah ketika berhadapan dengan bilangan-bilangan yang sangat besar. Mencari FPB dan KPK dari bilangan-bilangan tersebut secara manual dapat menjadi sangat memakan waktu dan rumit.
-
Keterbatasan Algoritma
Algoritma pencarian FPB dan KPK yang umum digunakan, seperti algoritma Euklidean, memiliki keterbatasan dalam hal efisiensi ketika diterapkan pada bilangan yang sangat besar. -
Kompleksitas Komputasi
Mencari FPB dan KPK dari bilangan-bilangan yang sangat besar dapat menjadi masalah komputasi yang kompleks, terutama untuk algoritma yang memerlukan waktu eksekusi yang lama. -
Aplikasi Praktis
Dalam beberapa aplikasi praktis, mungkin tidak selalu layak untuk mencari FPB dan KPK dari bilangan-bilangan yang sangat besar karena keterbatasan waktu dan sumber daya komputasi.
Meskipun terdapat tantangan dan keterbatasan tersebut, konsep FPB dan KPK tetap menjadi dasar penting dalam matematika dan memiliki banyak aplikasi yang luas. Memahami tantangan dan keterbatasan ini dapat membantu kita menggunakan konsep FPB dan KPK secara efektif dan efisien dalam berbagai konteks.
Pertanyaan Umum tentang FPB dan KPK
Berikut adalah beberapa pertanyaan umum beserta jawabannya terkait konsep Faktor Persekutuan Terbesar (FPB) dan Kelipatan Persekutuan Terkecil (KPK):
Pertanyaan 1: Apa perbedaan utama antara FPB dan KPK?
Jawaban: FPB adalah bilangan terbesar yang membagi habis dua atau lebih bilangan tanpa sisa, sedangkan KPK adalah bilangan terkecil yang habis dibagi oleh dua atau lebih bilangan. Jadi, FPB fokus pada faktor yang sama, sedangkan KPK fokus pada kelipatan yang sama.
Pertanyaan 2: Bagaimana cara mencari FPB dan KPK dari dua bilangan?
Jawaban: Ada beberapa cara untuk mencari FPB dan KPK, salah satunya adalah dengan menggunakan algoritma Euklidean. Algoritma ini bekerja dengan cara membagi bilangan yang lebih besar dengan bilangan yang lebih kecil berulang kali, hingga sisa pembagian menjadi 0. FPB dari dua bilangan adalah bilangan terakhir yang bukan 0 sebelum sisa pembagian menjadi 0, sedangkan KPK dari dua bilangan adalah hasil kali dari kedua bilangan dibagi dengan FPB.
Pertanyaan 3: Apa saja aplikasi FPB dan KPK dalam kehidupan sehari-hari?
Jawaban: FPB dan KPK memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti mencari satuan terkecil untuk mengisi wadah dengan ukuran berbeda, mencari waktu bersama terpendek yang memungkinkan beberapa orang untuk bertemu, dan mencari pembagian warisan yang adil.
Pertanyaan 4: Apakah ada keterbatasan dalam mencari FPB dan KPK?
Jawaban: Ya, ada keterbatasan dalam mencari FPB dan KPK, terutama ketika berhadapan dengan bilangan yang sangat besar. Mencari FPB dan KPK dari bilangan yang sangat besar secara manual dapat menjadi sangat memakan waktu dan rumit, sehingga perlu menggunakan algoritma yang efisien atau bantuan komputer.
Memahami konsep FPB dan KPK serta aplikasinya sangat penting untuk menguasai dasar-dasar matematika dan menyelesaikan berbagai permasalahan praktis dalam kehidupan sehari-hari.
Lanjut ke bagian artikel berikutnya…
Tips Memahami Faktor Persekutuan Terbesar dan Kelipatan Persekutuan Terkecil
Berikut adalah beberapa tips untuk membantu Anda memahami dan menguasai konsep Faktor Persekutuan Terbesar (FPB) dan Kelipatan Persekutuan Terkecil (KPK):
Tip 1: Pahami definisi dan sifat FPB dan KPK
FPB adalah bilangan terbesar yang membagi habis dua atau lebih bilangan tanpa sisa, sedangkan KPK adalah bilangan terkecil yang habis dibagi oleh dua atau lebih bilangan. Memahami definisi dan sifat dasar ini sangat penting untuk memahami konsep FPB dan KPK.
Tip 2: Kuasai algoritma mencari FPB dan KPK
Ada beberapa algoritma yang dapat digunakan untuk mencari FPB dan KPK, seperti algoritma Euklidean. Menguasai algoritma ini akan memudahkan Anda dalam menyelesaikan soal-soal terkait FPB dan KPK.
Tip 3: Latih soal-soal secara teratur
Latihan soal secara teratur akan membantu Anda memperkuat pemahaman dan meningkatkan kemampuan Anda dalam mencari FPB dan KPK. Carilah soal-soal dengan tingkat kesulitan yang bervariasi untuk menguji kemampuan Anda.
Tip 4: Terapkan FPB dan KPK dalam kehidupan sehari-hari
FPB dan KPK memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti mencari satuan terkecil untuk mengisi wadah dengan ukuran berbeda atau mencari waktu bersama terpendek yang memungkinkan beberapa orang untuk bertemu. Cobalah untuk menerapkan konsep FPB dan KPK dalam situasi praktis untuk meningkatkan pemahaman Anda.
Tip 5: Hubungkan FPB dan KPK dengan topik matematika lainnya
FPB dan KPK terkait dengan berbagai topik matematika lainnya, seperti teori bilangan, aljabar, dan geometri. Memahami hubungan ini akan membantu Anda melihat FPB dan KPK dari perspektif yang lebih luas dan memperkuat pemahaman Anda.
Dengan mengikuti tips ini, Anda dapat meningkatkan pemahaman dan keterampilan Anda dalam menghitung dan menerapkan FPB dan KPK. Konsep ini merupakan dasar penting dalam matematika dan memiliki banyak aplikasi dalam kehidupan sehari-hari.
Lanjut ke bagian artikel berikutnya…
Youtube Video: