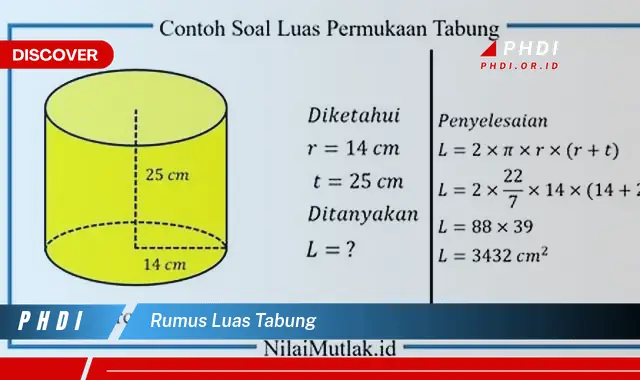
Rumus luas tabung adalah persamaan matematika yang digunakan untuk menghitung luas permukaan tabung. Luas tersebut merupakan jumlah luas selimut dan luas kedua alas lingkaran tabung. Rumus luas tabung dinyatakan sebagai:
Luas = 2r(r + t)
di mana:
- (pi) adalah konstanta matematika bernilai sekitar 3,14
- r adalah jari-jari alas lingkaran tabung
- t adalah tinggi tabung
Rumus luas tabung ini penting dalam berbagai bidang, seperti teknik, fisika, dan desain industri. Rumus ini digunakan untuk menghitung luas permukaan pipa, tangki, dan benda berbentuk tabung lainnya. Selain itu, rumus ini juga bermanfaat dalam menghitung volume dan kapasitas tabung.
Sejarah rumus luas tabung dapat ditelusuri kembali ke zaman kuno. Matematikawan Yunani Archimedes (287-212 SM) dipercaya telah mengembangkan rumus ini. Rumus tersebut kemudian disempurnakan oleh matematikawan dan ilmuwan sepanjang sejarah.
Rumus Luas Tabung
Rumus luas tabung merupakan persamaan matematika penting yang digunakan untuk menghitung luas permukaan tabung. Rumus ini memiliki berbagai aspek penting, di antaranya:
- Definisi: Persamaan matematika untuk menghitung luas permukaan tabung.
- Bentuk: 2r(r + t), di mana adalah konstanta matematika, r adalah jari-jari alas, dan t adalah tinggi tabung.
- Aplikasi: Menghitung luas permukaan pipa, tangki, dan benda berbentuk tabung lainnya.
- Sejarah: Dikembangkan oleh Archimedes pada zaman kuno.
- Manfaat: Membantu dalam perancangan dan pembuatan benda berbentuk tabung.
- Keterkaitan: Terkait dengan konsep luas permukaan dan volume tabung.
- Contoh: Tabung dengan jari-jari alas 5 cm dan tinggi 10 cm memiliki luas permukaan 314 cm.
Dengan memahami aspek-aspek penting dari rumus luas tabung, kita dapat mengaplikasikannya secara efektif dalam berbagai bidang. Rumus ini menjadi dasar perhitungan untuk merancang dan membuat benda berbentuk tabung yang optimal, seperti pipa, tangki, dan wadah lainnya.
Definisi
Definisi rumus luas tabung sebagai persamaan matematika untuk menghitung luas permukaan tabung merupakan dasar dari konsep ini. Rumus ini memungkinkan kita untuk menentukan luas seluruh permukaan tabung, termasuk luas selimut dan luas kedua alas lingkaran.
- Aspek Fundamental: Rumus luas tabung merupakan aspek fundamental dalam memahami sifat-sifat tabung dan menghitung berbagai aspeknya, seperti volume dan kapasitas.
- Aplikasi Praktis: Definisi ini memberikan landasan bagi aplikasi praktis rumus luas tabung dalam berbagai bidang, seperti teknik, arsitektur, dan desain industri.
- Perhitungan Akurat: Definisi yang jelas memastikan perhitungan luas permukaan tabung yang akurat, yang sangat penting untuk merancang dan membangun struktur serta benda berbentuk tabung.
- Pemahaman Konseptual: Definisi ini membantu membangun pemahaman konseptual yang kuat tentang rumus luas tabung dan peranannya dalam geometri dan matematika.
Dengan memahami definisi rumus luas tabung sebagai persamaan matematika untuk menghitung luas permukaan tabung, kita dapat mengaplikasikannya secara efektif untuk menyelesaikan masalah dan membuat keputusan yang tepat dalam berbagai konteks.
Bentuk
Bentuk rumus luas tabung, yaitu 2r(r + t), memiliki implikasi penting dalam memahami sifat dan penerapan rumus tersebut.
- Pengaruh Konstanta : Konstanta , yang nilainya sekitar 3,14, berperan penting dalam bentuk rumus. Konstanta ini memastikan bahwa luas tabung selalu proporsional dengan kuadrat jari-jari alasnya.
- Variabel Jari-jari Alas: Variabel r, yang mewakili jari-jari alas tabung, menunjukkan bahwa luas tabung bergantung pada ukuran alasnya. Semakin besar jari-jarinya, semakin besar pula luas permukaan tabung.
- Pengaruh Tinggi Tabung: Variabel t, yang mewakili tinggi tabung, menunjukkan bahwa luas tabung juga bergantung pada tinggi atau panjangnya. Semakin tinggi tabung, semakin besar pula luas permukaannya.
- Hubungan dengan Volume Tabung: Bentuk rumus luas tabung memiliki hubungan yang erat dengan rumus volume tabung. Dengan mengetahui luas permukaan tabung dan tingginya, kita dapat dengan mudah menghitung volume tabung menggunakan rumus V = rt.
Dengan memahami bentuk rumus luas tabung, yaitu 2r(r + t), kita dapat memperoleh pemahaman yang lebih dalam tentang sifat tabung dan menerapkan rumus tersebut secara efektif dalam berbagai konteks.
Aplikasi
Rumus luas tabung sangat penting dalam menghitung luas permukaan berbagai benda berbentuk tabung, seperti pipa, tangki, dan wadah lainnya. Menghitung luas permukaan tersebut sangat penting untuk:
- Perencanaan dan Desain: Luas permukaan tabung diperlukan untuk merencanakan dan mendesain benda berbentuk tabung secara optimal, seperti menentukan ukuran dan bentuk yang sesuai untuk memenuhi kebutuhan tertentu.
- Kapasitas dan Volume: Menghitung luas permukaan tabung membantu kita menentukan kapasitas dan volume benda tersebut. Dengan mengetahui luas permukaan dan tinggi tabung, kita dapat menggunakan rumus volume tabung (V = rt) untuk menghitung volumenya.
- Transfer Panas dan Perpindahan Massa: Luas permukaan tabung sangat penting dalam proses transfer panas dan perpindahan massa. Mengetahui luas permukaan tabung memungkinkan kita menghitung laju perpindahan panas dan massa, yang penting dalam aplikasi seperti penukar panas dan reaktor kimia.
- Struktur dan Kekuatan: Luas permukaan tabung juga berperan dalam menentukan kekuatan dan integritas struktural benda berbentuk tabung. Dengan menghitung luas permukaan, kita dapat menilai kemampuan tabung untuk menahan tekanan dan beban.
Dengan memahami aplikasi rumus luas tabung dalam menghitung luas permukaan pipa, tangki, dan benda berbentuk tabung lainnya, kita dapat mengoptimalkan desain, menentukan kapasitas, menganalisis perpindahan panas dan massa, serta memastikan kekuatan struktural benda-benda tersebut.
Sejarah
Hubungan antara sejarah pengembangan rumus luas tabung dengan Archimedes pada zaman kuno sangatlah penting. Archimedes, seorang matematikawan dan ilmuwan Yunani yang hidup pada abad ke-3 SM, memainkan peran penting dalam pengembangan rumus ini.
Salah satu pencapaian Archimedes yang paling terkenal adalah penemuan metode untuk menghitung luas dan volume benda-benda beraturan, termasuk tabung. Metode ini didasarkan pada prinsip-prinsip geometri dan kalkulus, yang pada saat itu belum sepenuhnya berkembang.
Archimedes menggunakan metodenya untuk mengembangkan rumus untuk menghitung luas permukaan tabung, yang kemudian dikenal sebagai rumus luas tabung. Rumus ini menyatakan bahwa luas permukaan tabung sama dengan dua kali hasil kali jari-jari alas tabung dengan jumlah jari-jari alas dan tinggi tabung. Dengan kata lain:
Luas permukaan tabung = 2r(r + t)
di mana:
- adalah konstanta matematika sekitar 3,14
- r adalah jari-jari alas tabung
- t adalah tinggi tabung
Rumus luas tabung yang dikembangkan oleh Archimedes ini sangat penting dalam berbagai bidang, seperti teknik, fisika, dan desain industri. Rumus ini digunakan untuk menghitung luas permukaan pipa, tangki, dan benda berbentuk tabung lainnya.
Manfaat
Rumus luas tabung sangat bermanfaat dalam perancangan dan pembuatan benda berbentuk tabung karena memberikan dasar matematis untuk menghitung luas permukaan benda tersebut. Hal ini penting untuk:
- Optimalisasi Desain: Rumus luas tabung memungkinkan para insinyur dan desainer mengoptimalkan desain benda berbentuk tabung, seperti pipa, tangki, dan wadah lainnya. Dengan menghitung luas permukaan secara akurat, mereka dapat menentukan ukuran dan bentuk yang optimal untuk memenuhi persyaratan fungsional dan estetika.
- Perkiraan Biaya Bahan: Luas permukaan tabung juga penting untuk memperkirakan biaya bahan yang diperlukan untuk pembuatan benda tersebut. Mengetahui luas permukaan yang tepat memungkinkan produsen menghitung jumlah bahan baku yang dibutuhkan, seperti logam, plastik, atau kaca.
- Analisis Struktural: Rumus luas tabung juga digunakan dalam analisis struktural benda berbentuk tabung. Dengan menghitung luas permukaan, insinyur dapat menilai kekuatan dan stabilitas struktur tabung, memastikan bahwa tabung dapat menahan beban dan tekanan yang diharapkan.
- Efisiensi Manufaktur: Dalam proses manufaktur, rumus luas tabung membantu mengoptimalkan efisiensi produksi. Dengan menghitung luas permukaan, produsen dapat menentukan jumlah bahan yang dibutuhkan dan merencanakan proses produksi secara efisien, sehingga meminimalkan limbah dan memaksimalkan produktivitas.
Dengan demikian, rumus luas tabung memberikan dasar yang penting untuk merancang, membuat, dan menganalisis benda berbentuk tabung secara efektif, berkontribusi pada efisiensi, keamanan, dan kinerja keseluruhan benda-benda tersebut.
Keterkaitan
Rumus luas tabung memiliki keterkaitan yang erat dengan konsep luas permukaan dan volume tabung. Luas permukaan tabung merupakan besaran yang penting untuk menentukan volume tabung. Volume tabung dapat dihitung dengan mengalikan luas permukaan tabung dengan tinggi tabung. Dengan demikian, rumus luas tabung menjadi dasar untuk menentukan volume tabung.
Selain itu, keterkaitan antara rumus luas tabung dengan konsep luas permukaan dan volume tabung juga terlihat pada aplikasi praktisnya. Dalam bidang teknik, misalnya, rumus luas tabung digunakan untuk menghitung luas permukaan dan volume pipa, tangki, dan wadah berbentuk tabung lainnya. Hal ini penting untuk memastikan kekuatan dan kapasitas struktur tabung tersebut.
Jadi, keterkaitan antara rumus luas tabung dengan konsep luas permukaan dan volume tabung sangatlah penting karena memungkinkan kita untuk memahami sifat tabung secara lebih komprehensif. Rumus luas tabung menjadi dasar untuk menghitung volume tabung dan memiliki aplikasi praktis yang luas dalam berbagai bidang.
Contoh
Contoh yang diberikan menunjukkan aplikasi praktis dari rumus luas tabung. Dengan menggunakan rumus Luas = 2r(r + t) dan memasukkan nilai jari-jari alas (r = 5 cm) dan tinggi tabung (t = 10 cm), kita dapat menghitung luas permukaan tabung sebagai berikut:
Luas = 2(5 cm)(5 cm + 10 cm) = 314 cm
Contoh ini menunjukkan bagaimana rumus luas tabung digunakan untuk menentukan luas permukaan tabung dengan ukuran tertentu. Contoh ini juga menyoroti pentingnya rumus luas tabung dalam aplikasi praktis, seperti menghitung luas permukaan pipa, tangki, dan wadah berbentuk tabung lainnya.
Tanya Jawab Umum
Berikut adalah beberapa tanya jawab umum terkait rumus luas tabung:
Pertanyaan 1: Apa itu rumus luas tabung?
Jawaban: Rumus luas tabung adalah persamaan matematika yang digunakan untuk menghitung luas permukaan tabung. Rumus ini menyatakan bahwa luas permukaan tabung sama dengan dua kali hasil kali jari-jari alas tabung dengan jumlah jari-jari alas dan tinggi tabung.
Pertanyaan 2: Bagaimana cara menggunakan rumus luas tabung?
Jawaban: Untuk menggunakan rumus luas tabung, kita perlu mengetahui jari-jari alas tabung dan tinggi tabung. Setelah itu, kita dapat mensubstitusikan nilai-nilai tersebut ke dalam rumus Luas = 2r(r + t) untuk menghitung luas permukaan tabung.
Pertanyaan 3: Apa saja aplikasi praktis dari rumus luas tabung?
Jawaban: Rumus luas tabung memiliki banyak aplikasi praktis, seperti dalam perancangan dan pembuatan pipa, tangki, dan wadah berbentuk tabung lainnya. Rumus ini juga digunakan dalam analisis struktural tabung untuk memastikan kekuatan dan kapasitasnya.
Pertanyaan 4: Bagaimana rumus luas tabung terkait dengan konsep luas permukaan dan volume tabung?
Jawaban: Rumus luas tabung terkait erat dengan konsep luas permukaan dan volume tabung. Luas permukaan tabung merupakan dasar untuk menghitung volume tabung. Volume tabung dapat dihitung dengan mengalikan luas permukaan tabung dengan tinggi tabung.
Dengan memahami rumus luas tabung dan aplikasinya, kita dapat menghitung luas permukaan tabung dengan akurat dan memanfaatkannya untuk berbagai keperluan praktis.
Lanjut ke bagian artikel berikutnya:
Tips Menghitung Luas Tabung
Berikut beberapa tips untuk membantu Anda menghitung luas tabung dengan lebih mudah dan akurat:
Tip 1: Pahami konsep luas tabung. Luas tabung adalah jumlah luas selimut dan luas kedua alas lingkaran tabung. Rumus untuk menghitung luas tabung adalah Luas = 2r(r + t), di mana adalah konstanta matematika sekitar 3,14, r adalah jari-jari alas tabung, dan t adalah tinggi tabung.
Tip 2: Pastikan Anda memiliki semua informasi yang diperlukan. Sebelum menghitung luas tabung, pastikan Anda mengetahui jari-jari alas dan tinggi tabung. Jika Anda tidak memiliki informasi ini, Anda perlu mengukurnya sendiri.
Tip 3: Gunakan kalkulator. Menghitung luas tabung bisa jadi rumit, terutama jika jari-jari alas dan tingginya besar. Menggunakan kalkulator dapat membantu Anda mendapatkan hasil yang akurat dengan cepat dan mudah.
Tip 4: Periksa kembali pekerjaan Anda. Setelah menghitung luas tabung, periksa kembali pekerjaan Anda untuk memastikan tidak ada kesalahan. Anda dapat melakukan ini dengan menghitung ulang luas tabung menggunakan metode yang berbeda atau dengan meminta orang lain untuk memeriksa pekerjaan Anda.
Tip 5: Terapkan dalam kehidupan nyata. Rumus luas tabung dapat diterapkan dalam berbagai situasi kehidupan nyata, seperti menghitung luas permukaan pipa, tangki, dan wadah berbentuk tabung lainnya. Memahami cara menghitung luas tabung sangat penting untuk berbagai aplikasi praktis.
Dengan mengikuti tips ini, Anda dapat menghitung luas tabung dengan lebih mudah dan akurat. Ingatlah untuk memahami konsep luas tabung, memiliki semua informasi yang diperlukan, menggunakan kalkulator, memeriksa kembali pekerjaan Anda, dan menerapkannya dalam kehidupan nyata.
Sekarang setelah Anda memahami cara menghitung luas tabung, Anda dapat melanjutkan ke bagian artikel berikutnya untuk mempelajari lebih lanjut tentang topik ini.
Youtube Video:










