Ketahui Rahasia Menghitung Median yang Jarang Diketahui

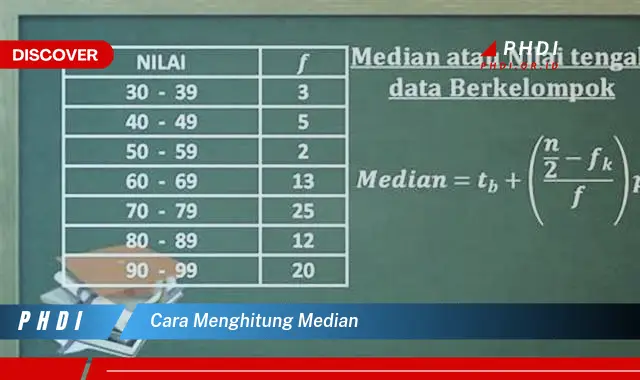
Median adalah nilai tengah dari suatu data yang telah diurutkan dari yang terkecil ke yang terbesar. Cara menghitung median dapat dilakukan dengan beberapa metode, tergantung pada jumlah data yang tersedia.

Jika jumlah data ganjil, maka median adalah nilai tengahnya. Misalnya, jika data yang tersedia adalah {1, 3, 5, 7, 9}, maka mediannya adalah 5. Sementara itu, jika jumlah data genap, maka median adalah rata-rata dari dua nilai tengahnya. Misalnya, jika data yang tersedia adalah {1, 3, 5, 7, 9, 11}, maka mediannya adalah (5 + 7) / 2 = 6.

Median memiliki beberapa kelebihan dibandingkan mean (rata-rata), yaitu tidak mudah dipengaruhi oleh nilai ekstrem (outlier) dan lebih mudah dipahami. Oleh karena itu, median sering digunakan dalam statistik untuk mewakili nilai tengah suatu data.

Daftar isi

Cara Menghitung Median

Pengertian Median: Nilai tengah suatu data yang telah diurutkan.
Jenis Data: Dapat diterapkan pada data numerik yang memiliki skala interval atau rasio.
Jumlah Data: Metode penghitungan berbeda untuk jumlah data ganjil dan genap.
Urutan Data: Data harus diurutkan dari terkecil ke terbesar.
Nilai Tengah: Untuk data ganjil, median adalah nilai tengah. Untuk data genap, median adalah rata-rata dua nilai tengah.
Ketahanan Outlier: Median tidak mudah dipengaruhi oleh nilai ekstrem (outlier).
Aplikasi: Digunakan untuk mewakili nilai tengah suatu data, terutama ketika terdapat outlier.

Pemahaman mendalam tentang aspek-aspek ini sangat penting untuk menghitung median secara akurat. Misalnya, jika kita memiliki data {1, 3, 5, 7, 9}, mediannya adalah 5 karena nilai tengah dari data yang telah diurutkan. Sementara itu, jika kita memiliki data {1, 3, 5, 7, 9, 11}, mediannya adalah (5 + 7) / 2 = 6 karena terdapat dua nilai tengah.

Pengertian Median

Konteks dalam Menghitung Median

Memahami konsep median sangat penting dalam konteks menghitung median. Median adalah nilai tengah dari suatu data yang telah diurutkan dari terkecil ke terbesar. Dengan memahami pengertian median ini, kita dapat menentukan langkah-langkah yang tepat dalam menghitung median suatu data.

Urutan Data:

Sebelum menghitung median, data harus diurutkan terlebih dahulu dari terkecil ke terbesar. Urutan data ini sangat krusial karena median bergantung pada posisi nilai tengah dalam data yang telah diurutkan.

Nilai Tengah:

Setelah data diurutkan, kita dapat menentukan nilai tengahnya. Jika jumlah data ganjil, maka median adalah nilai tengahnya. Jika jumlah data genap, maka median adalah rata-rata dari dua nilai tengahnya.

Dengan memahami hubungan antara pengertian median dan cara menghitung median, kita dapat memperoleh nilai tengah suatu data dengan tepat dan akurat. Memahami kedua aspek ini secara komprehensif akan membantu kita mengolah data numerik secara efektif.

Jenis Data

Dalam konteks cara menghitung median, jenis data yang dapat digunakan adalah data numerik yang memiliki skala interval atau rasio. Data numerik memiliki nilai yang dapat dikuantifikasi, sementara skala interval dan rasio memiliki sifat tertentu yang relevan dengan penghitungan median.

Skala Interval:

Skala interval memiliki jarak yang sama antara setiap nilai, tetapi tidak memiliki titik nol mutlak. Contoh data dengan skala interval adalah suhu (Celcius atau Fahrenheit) dan IQ.
Skala Rasio:

Skala rasio memiliki jarak yang sama antara setiap nilai dan memiliki titik nol mutlak. Contoh data dengan skala rasio adalah berat, tinggi, dan jumlah uang.

Jenis data ini penting dalam menghitung median karena median mewakili nilai tengah dari suatu data. Sifat jarak yang sama dan titik nol mutlak memungkinkan kita untuk membandingkan dan mengurutkan data numerik secara bermakna, sehingga median dapat dihitung dengan tepat.

Jumlah Data

Dalam konteks cara menghitung median, jumlah data yang tersedia menentukan metode penghitungan yang digunakan. Terdapat dua metode berbeda, tergantung apakah jumlah data ganjil atau genap.

Jumlah Data Ganjil:

Jika jumlah data ganjil, maka median adalah nilai tengah dari data yang telah diurutkan. Misalnya, jika data yang tersedia adalah {1, 3, 5, 7, 9}, maka mediannya adalah 5 karena nilai tengah dari data yang telah diurutkan.
Jumlah Data Genap:

Jika jumlah data genap, maka median adalah rata-rata dari dua nilai tengah dari data yang telah diurutkan. Misalnya, jika data yang tersedia adalah {1, 3, 5, 7, 9, 11}, maka mediannya adalah (5 + 7) / 2 = 6.

Mengetahui jumlah data yang tersedia sangat penting untuk menentukan metode penghitungan median yang tepat. Dengan memahami perbedaan metode ini, kita dapat memperoleh nilai tengah suatu data dengan akurat, baik untuk jumlah data ganjil maupun genap.

Urutan Data

Dalam konteks cara menghitung median, urutan data menjadi sangat penting karena median merupakan nilai tengah dari data yang telah diurutkan. Dengan mengurutkan data dari terkecil ke terbesar, kita dapat dengan mudah menentukan nilai tengah tersebut.

Proses pengurutan data memungkinkan kita untuk membandingkan nilai-nilai data secara sistematis dan mengidentifikasi nilai yang lebih kecil dan lebih besar. Setelah data diurutkan, kita dapat dengan jelas melihat posisi nilai tengah, yang merupakan median itu sendiri.

Oleh karena itu, urutan data menjadi komponen penting dalam cara menghitung median. Tanpa mengurutkan data terlebih dahulu, kita tidak akan dapat menentukan nilai tengah secara akurat, yang pada akhirnya akan menghasilkan median yang salah.

Nilai Tengah

Nilai tengah merupakan komponen penting dalam cara menghitung median. Median, yang merupakan nilai tengah dari suatu data, ditentukan berdasarkan nilai tengah tersebut. Jika jumlah data ganjil, nilai tengah adalah satu nilai yang berada di tengah setelah data diurutkan. Sebaliknya, jika jumlah data genap, nilai tengah adalah rata-rata dari dua nilai yang berada di tengah setelah data diurutkan.

Dengan memahami konsep nilai tengah ini, kita dapat menghitung median secara akurat. Nilai tengah menjadi acuan untuk menentukan posisi median dalam data yang telah diurutkan. Tanpa menentukan nilai tengah terlebih dahulu, kita tidak dapat memperoleh median yang tepat.

Jadi, pemahaman tentang nilai tengah sangat penting dalam cara menghitung median. Nilai tengah menjadi dasar penentuan median, yang mewakili nilai tengah dari suatu data.

Ketahanan Outlier

Dalam konteks cara menghitung median, ketahanan outlier merupakan aspek penting yang perlu dipahami. Median memiliki sifat yang tidak mudah dipengaruhi oleh nilai ekstrem (outlier), yang membedakannya dari nilai tengah lainnya seperti mean (rata-rata).

Pengaruh Outlier pada Mean:

Mean sangat mudah dipengaruhi oleh nilai ekstrem. Outlier dapat menarik mean ke arah nilainya, sehingga tidak lagi mewakili nilai tengah sebenarnya dari suatu data.
Pengaruh Outlier pada Median:

Median tidak mudah terpengaruh oleh outlier karena outlier tidak mengubah posisi nilai tengah dalam data yang telah diurutkan. Dengan demikian, median tetap menjadi representasi yang lebih stabil dari nilai tengah.
Contoh:

Misalkan kita memiliki data {1, 3, 5, 7, 100}. Mean data ini adalah 21,2 yang sangat dipengaruhi oleh nilai outlier 100. Sementara itu, median data ini adalah 5 yang tidak terpengaruh oleh outlier dan lebih mewakili nilai tengah sebenarnya.
Implikasi dalam Menghitung Median:

Ketahanan outlier menjadi pertimbangan penting dalam memilih metode penghitungan nilai tengah. Jika data mengandung outlier, median lebih disukai daripada mean karena memberikan representasi nilai tengah yang lebih akurat dan tidak menyesatkan.

Dengan memahami ketahanan outlier pada median, kita dapat memilih metode penghitungan nilai tengah yang tepat dan memperoleh representasi yang lebih akurat dari data yang kita miliki.

Aplikasi

Dalam konteks cara menghitung median, aplikasi median sangat penting karena median memiliki sifat yang tidak mudah dipengaruhi oleh nilai ekstrem (outlier). Sifat ini menjadikannya metode yang tepat untuk mewakili nilai tengah suatu data, terutama ketika data tersebut mengandung outlier.

Representasi Nilai Tengah:

Median merupakan representasi yang stabil dari nilai tengah suatu data karena tidak terpengaruh oleh outlier. Hal ini sangat penting ketika kita ingin mengetahui nilai tengah yang sebenarnya dari suatu data, tanpa adanya distorsi yang disebabkan oleh nilai ekstrem.
Contoh Aplikasi:

Median digunakan dalam berbagai aplikasi, seperti:
– Dalam statistik, median digunakan untuk membandingkan distribusi data yang berbeda.
– Dalam bidang keuangan, median digunakan untuk menghitung nilai rata-rata portofolio investasi.
– Dalam bidang kesehatan, median digunakan untuk menentukan nilai tengah dari hasil tes medis.
Pertimbangan dalam Menghitung Median:

Ketika menghitung median, penting untuk mempertimbangkan keberadaan outlier dalam data. Jika terdapat outlier, median akan memberikan representasi nilai tengah yang lebih akurat dibandingkan dengan metode nilai tengah lainnya, seperti mean (rata-rata).

Dengan memahami aplikasi median dalam mewakili nilai tengah suatu data, terutama ketika terdapat outlier, kita dapat memilih metode penghitungan nilai tengah yang tepat dan memperoleh representasi data yang akurat dan bermakna.

Pertanyaan Umum tentang Cara Menghitung Median

Berikut adalah beberapa pertanyaan umum seputar cara menghitung median:

Pertanyaan 1: Apa perbedaan antara median dan mean (rata-rata)?

Median adalah nilai tengah dari suatu data yang telah diurutkan, sedangkan mean adalah hasil penjumlahan semua nilai data dibagi dengan jumlah data. Median tidak mudah dipengaruhi oleh nilai ekstrem (outlier), sementara mean mudah terpengaruh oleh outlier.

Pertanyaan 2: Bagaimana cara menghitung median jika jumlah datanya ganjil?

Jika jumlah datanya ganjil, median adalah nilai tengah dari data yang telah diurutkan. Misalnya, jika data yang tersedia adalah {1, 3, 5, 7, 9}, maka mediannya adalah 5.

Pertanyaan 3: Bagaimana cara menghitung median jika jumlah datanya genap?

Jika jumlah datanya genap, median adalah rata-rata dari dua nilai tengah dari data yang telah diurutkan. Misalnya, jika data yang tersedia adalah {1, 3, 5, 7, 9, 11}, maka mediannya adalah (5 + 7) / 2 = 6.

Pertanyaan 4: Dalam situasi apa median lebih disukai daripada mean?

Median lebih disukai daripada mean ketika data mengandung outlier atau nilai ekstrem. Hal ini karena median tidak mudah dipengaruhi oleh outlier, sehingga memberikan representasi nilai tengah yang lebih akurat.

Dengan memahami pertanyaan umum ini, kita dapat memperoleh pemahaman yang lebih baik tentang cara menghitung median dan kapan metode ini lebih tepat digunakan.

Baca Juga: Pengertian dan Manfaat Median dalam Statistik

Tips Menghitung Median

Median adalah nilai tengah suatu data yang telah diurutkan dari yang terkecil ke yang terbesar. Berikut adalah beberapa tips untuk menghitung median dengan mudah dan akurat:

Tips 1: Urutkan data dari terkecil ke terbesar. Urutan data sangat penting untuk menentukan nilai tengah.

Tips 2: Jika jumlah data ganjil, median adalah nilai tengahnya. Misalnya, jika data yang tersedia adalah {1, 3, 5, 7, 9}, maka mediannya adalah 5.

Tips 3: Jika jumlah data genap, median adalah rata-rata dari dua nilai tengahnya. Misalnya, jika data yang tersedia adalah {1, 3, 5, 7, 9, 11}, maka mediannya adalah (5 + 7) / 2 = 6.

Tips 4: Median tidak mudah dipengaruhi oleh nilai ekstrem (outlier). Oleh karena itu, median lebih disukai daripada mean (rata-rata) ketika data mengandung outlier.

Tips 5: Median banyak digunakan dalam statistik untuk mewakili nilai tengah suatu data, terutama ketika terdapat outlier.

Dengan mengikuti tips-tips di atas, Anda dapat menghitung median dengan cepat dan akurat, sehingga dapat memperoleh pemahaman yang lebih baik tentang data yang Anda miliki.

Baca Juga: Pengertian dan Manfaat Median dalam Statistik