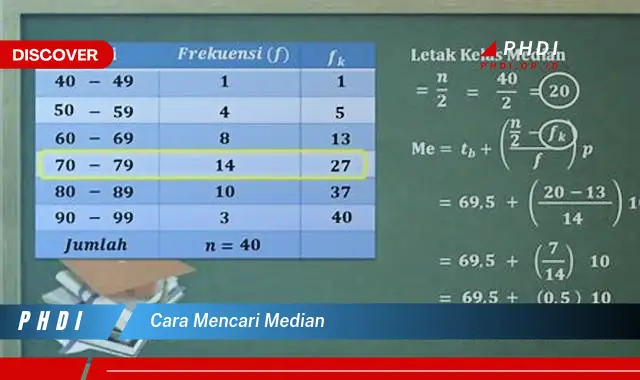
Cara mencari median adalah proses menentukan nilai tengah dari suatu kumpulan data yang telah diurutkan. Median membagi data menjadi dua bagian yang sama, di mana setengah dari data berada di bawah median dan setengah lainnya berada di atas median.
Median merupakan ukuran tendensi sentral yang penting karena tidak terpengaruh oleh nilai ekstrem dalam suatu kumpulan data. Hal ini menjadikannya ukuran yang lebih stabil dan representatif dibandingkan mean (rata-rata) ketika berhadapan dengan data yang memiliki nilai ekstrem atau pencilan.
Untuk mencari median, urutkan data dari yang terkecil hingga terbesar. Jika jumlah data ganjil, median adalah nilai tengah. Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah.
Cara Mencari Median
Median merupakan ukuran tendensi sentral yang penting dalam statistika, dan terdapat beberapa aspek penting dalam mencari median:
- Mengurutkan Data: Urutkan data dari yang terkecil hingga terbesar.
- Nilai Tengah: Jika jumlah data ganjil, median adalah nilai tengah.
- Rata-rata Nilai Tengah: Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah.
- Tidak Terpengaruh Nilai Ekstrem: Median tidak terpengaruh oleh nilai ekstrem dalam suatu kumpulan data.
- Ukuran Stabil: Median merupakan ukuran yang lebih stabil dan representatif dibandingkan mean (rata-rata) ketika berhadapan dengan data yang memiliki nilai ekstrem atau pencilan.
- Aplikasi Luas: Median memiliki aplikasi luas dalam berbagai bidang, seperti analisis data, penelitian ilmiah, dan pengambilan keputusan.
- Interpretasi Mudah: Median mudah diinterpretasikan dan dipahami, bahkan oleh orang awam.
Dengan memahami aspek-aspek penting tersebut, kita dapat mencari median secara akurat dan memanfaatkannya secara efektif dalam analisis data dan pengambilan keputusan.
Mengurutkan Data
Langkah awal dalam mencari median adalah mengurutkan data dari yang terkecil hingga terbesar. Proses pengurutan ini sangat penting karena membantu kita mengidentifikasi nilai tengah atau rata-rata nilai tengah, yang merupakan dasar perhitungan median.
Tanpa mengurutkan data, kita tidak dapat menentukan nilai tengah dengan akurat. Pengurutan memastikan bahwa nilai-nilai dalam kumpulan data tersusun secara berurutan, memungkinkan kita untuk membagi data menjadi dua bagian yang sama dan menentukan median sebagai nilai yang memisahkan kedua bagian tersebut.
Oleh karena itu, mengurutkan data merupakan komponen penting dalam cara mencari median, karena menyediakan dasar yang teratur untuk mengidentifikasi nilai tengah atau rata-rata nilai tengah yang menjadi dasar perhitungan median.
Nilai Tengah
Dalam konteks cara mencari median, pemahaman tentang nilai tengah sangat penting. Ketika jumlah data dalam suatu kumpulan data ganjil, median dapat langsung ditentukan sebagai nilai tengah.
- Mengidentifikasi Nilai Tengah: Ketika data diurutkan dari yang terkecil hingga terbesar, nilai tengah adalah nilai yang berada di tengah-tengah urutan tersebut. Nilai ini membagi data menjadi dua bagian yang sama, dengan setengah data berada di bawah nilai tengah dan setengah lainnya di atas nilai tengah.
- Contoh Nyata: Misalkan kita memiliki kumpulan data [3, 5, 7, 9, 11]. Setelah diurutkan, nilai tengahnya adalah 7. Ini berarti bahwa setengah dari data (nilai 3, 5) berada di bawah 7, dan setengah lainnya (nilai 9, 11) berada di atas 7.
- Implikasi dalam Penentuan Median: Ketika jumlah data ganjil, nilai tengah secara langsung mewakili median. Ini karena median membagi data menjadi dua bagian yang sama, dan nilai tengah sudah memenuhi kondisi tersebut.
Dengan memahami konsep nilai tengah, kita dapat menentukan median secara akurat ketika berhadapan dengan kumpulan data dengan jumlah data ganjil. Nilai tengah memberikan titik referensi yang jelas untuk membagi data dan mengidentifikasi nilai yang mewakili median.
Rata-rata Nilai Tengah
Dalam konteks cara mencari median, rata-rata nilai tengah memainkan peran penting ketika jumlah data dalam suatu kumpulan data genap. Ketika berhadapan dengan situasi ini, median tidak dapat langsung ditentukan sebagai satu nilai tengah seperti pada kasus jumlah data ganjil.
- Mengidentifikasi Dua Nilai Tengah: Ketika data diurutkan dari yang terkecil hingga terbesar, dua nilai tengah adalah nilai-nilai yang berada di tengah-tengah urutan tersebut. Kedua nilai ini membagi data menjadi dua bagian yang sama, dengan setengah data berada di bawah dua nilai tengah dan setengah lainnya di atas dua nilai tengah.
- Contoh Nyata: Misalkan kita memiliki kumpulan data [3, 5, 7, 9, 11, 13]. Setelah diurutkan, dua nilai tengahnya adalah 7 dan 9. Ini berarti bahwa setengah dari data (nilai 3, 5) berada di bawah 7 dan 9, dan setengah lainnya (nilai 11, 13) berada di atas 7 dan 9.
- Menghitung Rata-rata: Median, dalam kasus ini, dihitung sebagai rata-rata dari dua nilai tengah. Dalam contoh kita, mediannya adalah (7 + 9) / 2 = 8.
Dengan memahami konsep rata-rata nilai tengah, kita dapat menentukan median secara akurat ketika berhadapan dengan kumpulan data dengan jumlah data genap. Rata-rata nilai tengah memberikan dasar untuk menghitung median, yang merupakan nilai yang mewakili titik tengah dari data yang telah diurutkan.
Tidak Terpengaruh Nilai Ekstrem
Salah satu aspek penting dalam cara mencari median adalah sifatnya yang tidak terpengaruh oleh nilai ekstrem dalam suatu kumpulan data. Nilai ekstrem adalah nilai yang sangat tinggi atau sangat rendah yang dapat mendistorsi ukuran tendensi sentral lainnya, seperti mean (rata-rata).
Median, di sisi lain, tidak terpengaruh oleh nilai ekstrem karena merupakan nilai tengah dari data yang telah diurutkan. Artinya, nilai ekstrem yang jauh dari nilai tengah tidak akan memengaruhi posisi median. Hal ini menjadikan median ukuran yang lebih stabil dan representatif, terutama ketika berhadapan dengan data yang mengandung pencilan atau nilai ekstrem.
Sifat tidak terpengaruh nilai ekstrem sangat penting dalam cara mencari median karena memastikan bahwa median memberikan representasi yang akurat dari data yang mendasarinya. Dengan tidak terpengaruh oleh nilai ekstrem, median dapat memberikan ukuran tendensi sentral yang stabil dan dapat diandalkan, bahkan dalam kumpulan data yang memiliki variasi yang besar.
Ukuran Stabil
Sifat median yang stabil sangat penting dalam konteks cara mencari median karena memberikan dasar yang kuat untuk menentukan ukuran tendensi sentral yang akurat dan dapat diandalkan. Ketika berhadapan dengan data yang memiliki nilai ekstrem atau pencilan, median tidak terpengaruh oleh nilai-nilai tersebut, sehingga memberikan representasi yang lebih baik dari nilai tengah data yang sebenarnya.
Dengan kata lain, sifat stabil median membantu memastikan bahwa cara mencari median menghasilkan ukuran yang tidak terdistorsi oleh nilai ekstrem. Hal ini menjadikannya pilihan yang lebih tepat untuk menganalisis data yang mungkin mengandung pencilan atau nilai ekstrem yang dapat menyesatkan ukuran tendensi sentral lainnya, seperti mean (rata-rata).
Dengan demikian, sifat stabil median merupakan komponen penting dalam cara mencari median, karena memungkinkan penentuan ukuran tendensi sentral yang akurat dan representatif, terlepas dari adanya nilai ekstrem dalam data yang mendasarinya.
Aplikasi Luas
Pemahaman tentang cara mencari median sangat penting karena median memiliki aplikasi yang luas dalam berbagai bidang. Median digunakan secara ekstensif dalam analisis data karena sifatnya yang tidak terpengaruh oleh nilai ekstrem, menjadikannya ukuran tendensi sentral yang stabil dan representatif.
Dalam penelitian ilmiah, median digunakan untuk membandingkan kelompok data dan mengidentifikasi tren atau pola. Sifatnya yang tidak terpengaruh nilai ekstrem memastikan bahwa perbedaan antara kelompok tidak terdistorsi oleh nilai-nilai yang menyimpang.
Selain itu, median berperan penting dalam pengambilan keputusan, terutama ketika dihadapkan pada data yang mungkin mengandung pencilan atau nilai ekstrem. Dengan menggunakan median sebagai ukuran tendensi sentral, pembuat keputusan dapat membuat keputusan yang lebih tepat dan terinformasi, karena tidak akan terpengaruh oleh nilai-nilai yang menyimpang.
Interpretasi Mudah
Interpretasi mudah merupakan aspek penting dalam cara mencari median karena memungkinkan pemahaman yang jelas dan intuitif tentang hasil yang diperoleh. Median, sebagai ukuran tendensi sentral, disajikan dalam bentuk nilai tunggal yang mewakili titik tengah data.
Sifat median yang mudah diinterpretasikan menjadikannya alat yang berharga untuk mengomunikasikan temuan data kepada audiens yang beragam, termasuk mereka yang mungkin tidak memiliki latar belakang statistik yang kuat. Median memberikan gambaran yang sederhana dan mudah dipahami tentang nilai tengah data, tanpa kerumitan perhitungan atau konsep statistik yang kompleks.
Dengan demikian, interpretasi mudah dari median berkontribusi pada efektivitas cara mencari median sebagai metode untuk menganalisis dan memahami data. Hal ini memungkinkan pengguna untuk memperoleh wawasan yang jelas dan bermakna dari data mereka, memfasilitasi pengambilan keputusan yang tepat dan pemahaman yang komprehensif.
Pertanyaan Umum tentang Cara Mencari Median
Berikut beberapa pertanyaan umum dan jawabannya terkait cara mencari median:
Pertanyaan 1: Apa itu median?
Jawaban: Median adalah nilai tengah dalam suatu kumpulan data yang telah diurutkan. Median membagi data menjadi dua bagian yang sama, dengan setengah data berada di bawah median dan setengah lainnya berada di atas median.
Pertanyaan 2: Bagaimana cara mencari median jika jumlah datanya ganjil?
Jawaban: Jika jumlah data ganjil, median adalah nilai tengah dari data yang telah diurutkan.
Pertanyaan 3: Bagaimana cara mencari median jika jumlah datanya genap?
Jawaban: Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah dari data yang telah diurutkan.
Pertanyaan 4: Mengapa median lebih baik daripada mean (rata-rata) ketika berhadapan dengan data yang memiliki nilai ekstrem?
Jawaban: Median tidak terpengaruh oleh nilai ekstrem, sehingga menjadikannya ukuran tendensi sentral yang lebih stabil dan representatif ketika berhadapan dengan data yang memiliki pencilan atau nilai ekstrem.
Dengan memahami pertanyaan umum ini, Anda dapat memperoleh pemahaman yang lebih baik tentang cara mencari median dan menerapkannya secara efektif dalam analisis data.
Kembali ke Bagian Utama Artikel
Cara Mencari Median
Memahami cara mencari median sangat penting untuk menganalisis dan menafsirkan data secara efektif. Berikut beberapa tip dan trik untuk membantu Anda menguasai teknik ini:
Tip 1: Pahami Konsep Nilai Tengah
Sebelum mencari median, penting untuk memahami konsep nilai tengah. Nilai tengah adalah nilai yang berada di tengah-tengah data yang telah diurutkan. Dalam kasus jumlah data ganjil, nilai tengah langsung mewakili median. Dalam kasus jumlah data genap, median adalah rata-rata dari dua nilai tengah.
Tip 2: Urutkan Data dengan Benar
Mengurutkan data dengan benar sangat penting untuk menentukan median yang akurat. Data harus diurutkan dari yang terkecil hingga terbesar atau sebaliknya, tergantung pada kebutuhan analisis Anda.
Tip 3: Perhatikan Jumlah Data
Jumlah data mempengaruhi cara mencari median. Jika jumlah data ganjil, median adalah nilai tengah. Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah.
Tip 4: Visualisasikan Data
Memvisualisasikan data menggunakan grafik atau bagan dapat membantu Anda memahami distribusi data dan mengidentifikasi median dengan lebih mudah. Grafik batang dan histogram sangat berguna untuk memvisualisasikan median.
Tip 5: Gunakan Kalkulator atau Perangkat Lunak Statistik
Jika Anda berhadapan dengan kumpulan data yang besar, menggunakan kalkulator atau perangkat lunak statistik dapat mempermudah proses pencarian median. Alat-alat ini dapat menghitung median secara otomatis, menghemat waktu dan meminimalkan kesalahan.
Dengan mengikuti tip dan trik ini, Anda dapat meningkatkan keterampilan Anda dalam mencari median dan memanfaatkan teknik ini secara efektif untuk menganalisis dan memahami data.
Kesimpulannya, memahami cara mencari median sangat penting untuk menganalisis data secara akurat dan komprehensif. Dengan menerapkan tip dan trik yang telah dibahas, Anda dapat memperoleh wawasan yang berharga dari data Anda dan membuat keputusan yang tepat.
Youtube Video:










