Intip Rumus Jajar Genjang yang Jarang Diketahui

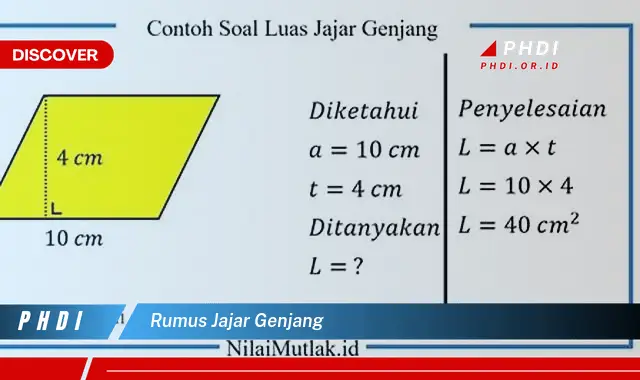
Rumus jajar genjang adalah rumus yang digunakan untuk menghitung luas dan keliling jajar genjang. Rumus luas jajar genjang adalah hasil perkalian antara alas dan tinggi, sedangkan rumus keliling jajar genjang adalah hasil penjumlahan panjang keempat sisinya.

Rumus jajar genjang sangat penting dalam matematika dan memiliki banyak manfaat. Rumus ini dapat digunakan untuk menghitung luas dan keliling lahan, bangunan, dan benda-benda lainnya yang berbentuk jajar genjang. Rumus ini juga dapat digunakan untuk menyelesaikan masalah matematika, seperti menghitung luas taman atau menghitung keliling lapangan.

Rumus jajar genjang telah digunakan selama berabad-abad dan memiliki sejarah yang panjang. Rumus ini pertama kali ditemukan oleh matematikawan Yunani kuno, Pythagoras. Rumus ini kemudian dikembangkan lebih lanjut oleh matematikawan Arab dan Eropa pada Abad Pertengahan. Rumus jajar genjang yang kita gunakan sekarang ini adalah hasil pengembangan dari matematikawan selama berabad-abad.

rumus jajar genjang

Rumus jajar genjang adalah rumus yang penting dalam matematika. Rumus ini memiliki banyak aspek penting, antara lain:

• Luas
• Keliling
• Alas
• Tinggi
• Diagonal
• Sudut
• Sejarah

Luas dan keliling jajar genjang dapat dihitung menggunakan rumus yang melibatkan alas dan tinggi. Diagonal jajar genjang membagi jajar genjang menjadi dua segitiga siku-siku. Sudut-sudut jajar genjang berhadapan sama besar. Rumus jajar genjang memiliki sejarah yang panjang, dan telah digunakan selama berabad-abad untuk menghitung luas dan keliling lahan, bangunan, dan benda-benda lainnya yang berbentuk jajar genjang.

Luas

Luas adalah besaran yang menyatakan ukuran suatu permukaan. Dalam konteks rumus jajar genjang, luas jajar genjang dihitung dengan mengalikan alas dan tinggi jajar genjang.

• Cara Menghitung Luas Jajar Genjang

  Untuk menghitung luas jajar genjang, kita dapat menggunakan rumus: Luas = alas x tinggi. Misalnya, jika sebuah jajar genjang memiliki alas 10 cm dan tinggi 5 cm, maka luas jajar genjang tersebut adalah 50 cm².

• Manfaat Menghitung Luas Jajar Genjang

  Rumus luas jajar genjang dapat digunakan untuk menghitung luas berbagai benda yang berbentuk jajar genjang, seperti lantai, dinding, dan atap. Dengan mengetahui luas suatu benda, kita dapat merencanakan dan menggunakan ruang dengan lebih efisien.

• Hubungan Luas dengan Rumus Jajar Genjang

  Rumus luas jajar genjang merupakan bagian penting dari rumus jajar genjang secara keseluruhan. Luas jajar genjang digunakan untuk menghitung berbagai besaran lainnya, seperti keliling dan diagonal jajar genjang.

• Contoh Soal Luas Jajar Genjang

  Sebuah jajar genjang memiliki alas 12 cm dan tinggi 8 cm. Berapakah luas jajar genjang tersebut? Jawaban: Luas jajar genjang = alas x tinggi = 12 cm x 8 cm = 96 cm².

Dengan memahami luas jajar genjang dan cara menghitungnya, kita dapat menyelesaikan berbagai masalah matematika yang melibatkan bangun datar ini. Rumus luas jajar genjang merupakan alat yang penting untuk memahami geometri dan menyelesaikan masalah-masalah praktis.

Keliling

Keliling merupakan besaran yang menyatakan panjang batas suatu bangun datar. Dalam konteks rumus jajar genjang, keliling jajar genjang dihitung dengan menjumlahkan panjang keempat sisinya. Keliling jajar genjang penting karena memberikan informasi tentang panjang batas jajar genjang, yang berguna untuk berbagai keperluan praktis.

Keliling jajar genjang dapat digunakan untuk menghitung panjang pagar yang dibutuhkan untuk mengelilingi sebidang tanah berbentuk jajar genjang, menghitung panjang pita yang dibutuhkan untuk membungkus sebuah kado berbentuk jajar genjang, dan menghitung panjang tali yang dibutuhkan untuk mengikat sebuah benda berbentuk jajar genjang.

Rumus keliling jajar genjang merupakan bagian penting dari rumus jajar genjang secara keseluruhan. Keliling jajar genjang digunakan untuk menghitung berbagai besaran lainnya, seperti luas dan diagonal jajar genjang.

Dengan memahami keliling jajar genjang dan cara menghitungnya, kita dapat menyelesaikan berbagai masalah matematika yang melibatkan bangun datar ini. Rumus keliling jajar genjang merupakan alat yang penting untuk memahami geometri dan menyelesaikan masalah-masalah praktis.

Alas

Dalam rumus jajar genjang, alas merupakan salah satu besaran penting yang digunakan untuk menghitung luas dan keliling jajar genjang. Alas jajar genjang adalah sisi sejajar yang digunakan sebagai dasar dalam perhitungan luas dan keliling.

• Peranan Alas dalam Rumus Luas Jajar Genjang

  Dalam rumus luas jajar genjang, alas berperan sebagai faktor pengali yang dikalikan dengan tinggi jajar genjang. Artinya, besar alas akan mempengaruhi besarnya luas jajar genjang.

• Peranan Alas dalam Rumus Keliling Jajar Genjang

  Dalam rumus keliling jajar genjang, alas berperan sebagai salah satu sisi yang dijumlahkan dengan tiga sisi lainnya. Artinya, besar alas akan mempengaruhi besarnya keliling jajar genjang.

• Contoh Penerapan Alas dalam Rumus Jajar Genjang

  Misalnya, jika sebuah jajar genjang memiliki alas 10 cm dan tinggi 5 cm, maka luas jajar genjang tersebut adalah 50 cm². Sementara itu, jika jajar genjang tersebut memiliki alas 10 cm dan sisi lainnya 6 cm, maka keliling jajar genjang tersebut adalah 32 cm.

• Implikasi Penting Alas dalam Rumus Jajar Genjang

  Memahami peranan alas dalam rumus jajar genjang sangat penting untuk dapat menghitung luas dan keliling jajar genjang dengan benar. Kesalahan dalam menentukan alas dapat menyebabkan kesalahan dalam perhitungan luas dan keliling jajar genjang.

Dengan memahami hubungan antara alas dan rumus jajar genjang, kita dapat lebih mudah menyelesaikan masalah matematika yang melibatkan bangun datar ini. Alas merupakan komponen penting dalam rumus jajar genjang yang perlu diperhatikan dengan cermat untuk mendapatkan hasil perhitungan yang akurat.

Tinggi

Tinggi merupakan salah satu unsur penting dalam rumus jajar genjang karena berperan dalam menentukan luas dan keliling jajar genjang. Berikut adalah beberapa aspek penting terkait tinggi dalam konteks rumus jajar genjang:

• Peranan Tinggi dalam Rumus Luas Jajar Genjang

  Tinggi berperan sebagai pengali bersama alas dalam menghitung luas jajar genjang. Semakin besar tinggi jajar genjang, semakin besar pula luasnya.

• Peranan Tinggi dalam Rumus Keliling Jajar Genjang

  Tinggi tidak berperan langsung dalam rumus keliling jajar genjang karena keliling hanya melibatkan penjumlahan panjang keempat sisinya.

• Contoh Penerapan Tinggi dalam Rumus Jajar Genjang

  Misalnya, jika sebuah jajar genjang memiliki alas 10 cm dan tinggi 5 cm, maka luas jajar genjang tersebut adalah 50 cm².

• Implikasi Penting Tinggi dalam Rumus Jajar Genjang

  Memahami hubungan antara tinggi dan rumus jajar genjang sangat penting untuk dapat menghitung luas jajar genjang dengan benar. Kesalahan dalam menentukan tinggi dapat menyebabkan kesalahan dalam perhitungan luas jajar genjang.

Dengan memahami hubungan antara tinggi dan rumus jajar genjang, kita dapat lebih mudah menyelesaikan masalah matematika yang melibatkan bangun datar ini. Tinggi merupakan komponen penting dalam rumus jajar genjang yang perlu diperhatikan dengan cermat untuk mendapatkan hasil perhitungan yang akurat.

Diagonal

Diagonal jajar genjang merupakan ruas garis yang menghubungkan dua titik sudut yang berlawanan pada jajar genjang. Diagonal jajar genjang memiliki beberapa sifat penting yang berkaitan dengan rumus jajar genjang.

Salah satu sifat penting diagonal jajar genjang adalah membagi jajar genjang menjadi dua segitiga siku-siku yang kongruen. Hal ini berarti diagonal jajar genjang saling membagi sama panjang dan membentuk sudut siku-siku di titik potongnya.

Sifat diagonal jajar genjang tersebut memiliki implikasi penting dalam rumus jajar genjang. Misalnya, diagonal jajar genjang dapat digunakan untuk menentukan luas jajar genjang. Luas jajar genjang dapat dihitung dengan mengalikan setengah hasil kali panjang kedua diagonal jajar genjang. Selain itu, diagonal jajar genjang juga dapat digunakan untuk menentukan keliling jajar genjang. Keliling jajar genjang dapat dihitung dengan mengalikan setengah jumlah panjang kedua diagonal jajar genjang dengan 2.

Dengan memahami sifat-sifat diagonal jajar genjang dan hubungannya dengan rumus jajar genjang, kita dapat lebih mudah menyelesaikan masalah matematika yang melibatkan bangun datar ini. Diagonal jajar genjang merupakan komponen penting dalam rumus jajar genjang yang perlu dipahami dengan baik untuk mendapatkan hasil perhitungan yang akurat.

Sudut

Dalam rumus jajar genjang, sudut merupakan aspek penting yang berkaitan dengan sifat-sifat dan perhitungan jajar genjang. Sudut pada jajar genjang memiliki beberapa karakteristik dan implikasi yang perlu dipahami.

• Sudut Berhadapan Sama Besar

  Dalam jajar genjang, sudut-sudut yang berhadapan memiliki besar yang sama. Misalnya, jika salah satu sudut jajar genjang berukuran 60 derajat, maka sudut yang berhadapan dengannya juga berukuran 60 derajat.

• Sudut Dalam Sejumlah 360 Derajat

  Jumlah keempat sudut dalam pada jajar genjang adalah 360 derajat. Hal ini berlaku untuk semua jajar genjang, terlepas dari ukuran atau bentuknya.

• Hubungan dengan Diagonal

  Diagonal jajar genjang saling membagi sama panjang dan membentuk sudut siku-siku di titik potongnya. Artinya, sudut-sudut yang berdekatan dengan titik potong diagonal tersebut adalah sudut siku-siku.

• Implikasi dalam Perhitungan

  Sifat-sifat sudut jajar genjang dapat digunakan untuk menyelesaikan berbagai masalah matematika. Misalnya, sifat sudut berhadapan sama besar dapat digunakan untuk menentukan besar sudut yang tidak diketahui pada jajar genjang.

Dengan memahami sifat-sifat sudut jajar genjang dan hubungannya dengan rumus jajar genjang, kita dapat lebih mudah menyelesaikan masalah matematika yang melibatkan bangun datar ini. Sudut merupakan komponen penting dalam rumus jajar genjang yang perlu diperhatikan dengan baik untuk mendapatkan hasil perhitungan yang akurat.

Sejarah

Sejarah memiliki hubungan yang erat dengan rumus jajar genjang. Perkembangan rumus jajar genjang tidak terlepas dari perjalanan panjang sejarah matematika. Rumus jajar genjang yang kita gunakan saat ini merupakan hasil pengembangan dan penyempurnaan yang dilakukan oleh para matematikawan selama berabad-abad.

Rumus jajar genjang pertama kali ditemukan oleh matematikawan Yunani kuno, Pythagoras. Pythagoras menemukan rumus untuk menghitung luas jajar genjang, yang kemudian dikenal sebagai Teorema Pythagoras. Teorema Pythagoras menyatakan bahwa luas jajar genjang sama dengan hasil kali alas dan tinggi jajar genjang.

Setelah Pythagoras, matematikawan lain seperti Euclid dan Archimedes melanjutkan pengembangan rumus jajar genjang. Mereka mengembangkan rumus-rumus baru dan membuktikan sifat-sifat jajar genjang. Rumus-rumus ini kemudian menjadi dasar bagi perkembangan matematika selanjutnya, termasuk kalkulus dan geometri analitik.

Pada abad ke-17, matematikawan seperti Ren Descartes dan Pierre de Fermat mengembangkan konsep koordinat dan aljabar. Konsep-konsep ini memungkinkan pengembangan rumus jajar genjang dalam bentuk aljabar, yang lebih mudah digunakan untuk menyelesaikan masalah matematika.

Seiring berjalannya waktu, rumus jajar genjang terus disempurnakan dan digunakan untuk berbagai aplikasi dalam sains, teknik, dan bidang lainnya. Rumus jajar genjang menjadi salah satu dasar penting dalam matematika dan terus digunakan hingga saat ini.

Pertanyaan Umum tentang Rumus Jajar Genjang

Rumus jajar genjang merupakan salah satu konsep dasar dalam matematika yang digunakan untuk menghitung luas dan keliling jajar genjang. Berikut adalah beberapa pertanyaan umum dan jawabannya terkait rumus jajar genjang:

Pertanyaan 1: Bagaimana cara menghitung luas jajar genjang?

Jawaban: Luas jajar genjang dihitung dengan mengalikan alas dengan tinggi jajar genjang.

Pertanyaan 2: Bagaimana cara menghitung keliling jajar genjang?

Jawaban: Keliling jajar genjang dihitung dengan menjumlahkan panjang keempat sisinya.

Pertanyaan 3: Apa saja sifat-sifat diagonal jajar genjang?

Jawaban: Diagonal jajar genjang saling membagi sama panjang dan membentuk sudut siku-siku di titik potongnya.

Pertanyaan 4: Bagaimana sejarah perkembangan rumus jajar genjang?

Jawaban: Rumus jajar genjang pertama kali ditemukan oleh Pythagoras, dan terus dikembangkan oleh matematikawan lain seperti Euclid, Archimedes, Descartes, dan Fermat.

Dengan memahami rumus jajar genjang dan sifat-sifatnya, kita dapat menyelesaikan berbagai masalah matematika yang melibatkan bangun datar ini dengan lebih mudah.

Untuk mempelajari lebih lanjut tentang rumus jajar genjang, silakan merujuk ke artikel lengkap yang disediakan.

Tips Penting tentang Rumus Jajar Genjang

Rumus jajar genjang merupakan konsep penting dalam matematika yang digunakan untuk menyelesaikan berbagai masalah yang melibatkan bangun datar ini. Berikut adalah beberapa tips penting untuk membantu Anda memahami dan menggunakan rumus jajar genjang:

1. Pahami Konsep Dasar
Langkah pertama untuk menggunakan rumus jajar genjang adalah memahami konsep dasar yang mendasarinya. Pastikan Anda memahami apa itu jajar genjang, bagaimana menghitung luas dan kelilingnya, dan sifat-sifat pentingnya.

2. Hafalkan Rumus
Rumus jajar genjang sangat sederhana dan mudah dihafal. Luas jajar genjang dihitung dengan mengalikan alas dan tinggi, sedangkan kelilingnya dihitung dengan menjumlahkan panjang keempat sisinya.

3. Latihan Soal
Cara terbaik untuk menguasai rumus jajar genjang adalah dengan berlatih soal sebanyak mungkin. Carilah soal-soal latihan dari berbagai sumber, seperti buku teks, soal ujian, atau internet.

4. Gunakan Kalkulator
Dalam beberapa kasus, Anda mungkin perlu menggunakan kalkulator untuk menghitung luas atau keliling jajar genjang. Pastikan Anda memasukkan angka dengan benar dan memahami cara menggunakan kalkulator dengan baik.

5. Periksa Kembali Jawaban Anda
Setelah menghitung luas atau keliling jajar genjang, selalu periksa kembali jawaban Anda. Pastikan jawaban Anda masuk akal dan sesuai dengan sifat-sifat jajar genjang.

6. Manfaatkan Sumber Daya yang Ada
Jika Anda kesulitan memahami rumus jajar genjang, jangan ragu untuk mencari bantuan. Ada banyak sumber daya yang tersedia, seperti buku teks, guru, atau internet. Manfaatkan sumber daya ini untuk memperjelas pemahaman Anda.

Dengan mengikuti tips ini, Anda dapat memahami dan menggunakan rumus jajar genjang dengan lebih efektif. Rumus ini merupakan alat penting dalam matematika dan memiliki banyak aplikasi dalam kehidupan nyata.

Untuk mempelajari lebih lanjut tentang rumus jajar genjang, silakan merujuk ke artikel lengkap yang disediakan.

Youtube Video: