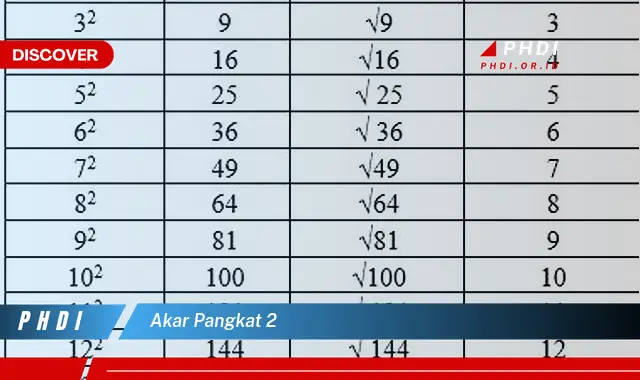
Akar pangkat 2, yang juga dikenal sebagai akar kuadrat, adalah operasi matematika yang digunakan untuk mencari nilai yang, ketika dikalikan dengan dirinya sendiri, menghasilkan bilangan asli. Misalnya, akar pangkat 2 dari 9 adalah 3, karena 3 x 3 = 9.
Akar pangkat 2 memiliki banyak aplikasi dalam matematika dan sains. Misalnya, akar pangkat 2 dapat digunakan untuk mencari panjang sisi miring segitiga siku-siku, atau untuk menghitung kecepatan sebuah benda yang jatuh bebas. Akar pangkat 2 juga digunakan dalam banyak persamaan fisika dan teknik.
Konsep akar pangkat 2 telah dikenal sejak zaman kuno. Orang Babilonia menggunakan akar pangkat 2 untuk menghitung panjang diagonal persegi panjang, dan orang Yunani menggunakannya untuk memecahkan masalah geometri. Akar pangkat 2 juga telah dipelajari oleh matematikawan India dan Arab, dan saat ini merupakan salah satu operasi matematika yang paling dasar dan penting.
Akar Pangkat 2
Akar pangkat 2, atau akar kuadrat, merupakan operasi matematika penting yang memiliki beragam aspek:
- Definisi: Operasi untuk mencari nilai yang dikalikan dengan dirinya sendiri menghasilkan bilangan asli
- Notasi: Dilambangkan dengan simbol
- Sifat: Selalu menghasilkan dua nilai, satu positif dan satu negatif (kecuali untuk 0)
- Aplikasi: Digunakan dalam berbagai bidang, seperti geometri, fisika, dan teknik
- Sejarah: Dikenal sejak zaman kuno, digunakan oleh berbagai peradaban
- Rumus: (a) = |a|, di mana a adalah bilangan real
- Kaitan: Berhubungan erat dengan konsep kuadrat dan pangkat dua
Pemahaman tentang aspek-aspek ini sangat penting karena akar pangkat 2 banyak digunakan dalam matematika dan sains. Misalnya, dalam geometri, akar pangkat 2 digunakan untuk menghitung panjang sisi miring segitiga siku-siku. Dalam fisika, akar pangkat 2 digunakan untuk menghitung kecepatan benda yang jatuh bebas. Dengan memahami sifat dan aplikasinya, kita dapat memanfaatkan akar pangkat 2 secara efektif untuk memecahkan berbagai masalah.
Definisi
Definisi ini merupakan dasar dari konsep akar pangkat 2. Operasi akar pangkat 2 bertujuan untuk menemukan nilai yang, ketika dikalikan dengan dirinya sendiri, menghasilkan bilangan asli yang diberikan. Misalnya, akar pangkat 2 dari 9 adalah 3 karena 3 x 3 = 9. Definisi ini sangat penting karena memberikan pemahaman yang jelas tentang tujuan dan mekanisme operasi akar pangkat 2.
Notasi
Notasi akar pangkat 2 yang menggunakan simbol memiliki peran penting dalam matematika. Simbol ini menunjukkan secara eksplisit operasi akar pangkat 2 yang akan dilakukan pada suatu bilangan atau ekspresi matematika.
-
Menunjukkan Operasi Akar Pangkat 2
Simbol secara jelas menunjukkan bahwa bilangan atau ekspresi di dalamnya akan dioperasikan dengan akar pangkat 2. Notasi ini membedakan operasi akar pangkat 2 dari operasi matematika lainnya, sehingga tidak terjadi kesalahan interpretasi. -
Menghindari Kesalahan Tanda
Akar pangkat 2 dapat menghasilkan dua nilai, yaitu positif dan negatif. Notasi dengan simbol membantu menghindari kesalahan tanda. Dengan menggunakan simbol ini, nilai positif dari akar pangkat 2 akan selalu diambil, kecuali dinyatakan sebaliknya. -
Memudahkan Penulisan
Simbol memudahkan penulisan operasi akar pangkat 2. Tanpa simbol ini, penulisan akar pangkat 2 akan lebih rumit dan memakan tempat, terutama untuk ekspresi matematika yang kompleks. -
Standarisasi Notasi
Notasi telah menjadi standar internasional untuk mewakili operasi akar pangkat 2. Konsistensi notasi ini memudahkan komunikasi matematika di seluruh dunia, menghilangkan kebingungan akibat perbedaan notasi.
Dengan demikian, notasi akar pangkat 2 dengan simbol sangat penting karena menunjukkan operasi akar pangkat 2 secara jelas, menghindari kesalahan tanda, memudahkan penulisan, dan menstandarisasi notasi matematika.
Sifat
Salah satu sifat unik dari akar pangkat 2 adalah selalu menghasilkan dua nilai, satu positif dan satu negatif. Sifat ini sangat penting dalam memahami dan mengaplikasikan operasi akar pangkat 2.
-
Dua Akar yang Berlawanan Tanda
Setiap bilangan positif memiliki dua akar pangkat 2, yaitu satu positif dan satu negatif. Misalnya, akar pangkat 2 dari 9 adalah 3 dan -3, karena 3 x 3 = 9 dan (-3) x (-3) = 9. Sifat ini menunjukkan bahwa akar pangkat 2 tidak hanya memberikan nilai positif, tetapi juga nilai negatif yang merupakan kebalikan dari nilai positif. -
Nilai Negatif untuk Bilangan Negatif
Jika bilangan yang dioperasikan akar pangkat 2 adalah negatif, maka akar pangkat 2 akan menghasilkan bilangan imajiner. Bilangan imajiner adalah bilangan yang mengandung satuan i, yaitu akar pangkat 2 dari -1. Misalnya, akar pangkat 2 dari -9 adalah 3i, karena 3i x 3i = -9. -
Pengecualian untuk 0
Satu-satunya pengecualian dari sifat ini adalah bilangan 0. Akar pangkat 2 dari 0 adalah 0, yang tidak memiliki nilai positif atau negatif.
Pemahaman sifat ini sangat penting dalam menyelesaikan persamaan dan pertidaksamaan yang melibatkan akar pangkat 2. Dengan mempertimbangkan kedua nilai akar pangkat 2 yang dihasilkan, kita dapat memperoleh solusi yang lengkap dan akurat.
Aplikasi
Akar pangkat 2 memiliki banyak aplikasi di berbagai bidang, mulai dari geometri dasar hingga fisika dan teknik tingkat lanjut.
-
Geometri
Dalam geometri, akar pangkat 2 digunakan untuk menghitung panjang sisi miring segitiga siku-siku menggunakan Teorema Pythagoras. Misalnya, jika panjang kedua sisi siku-siku sebuah segitiga adalah 3 cm dan 4 cm, maka panjang sisi miringnya dapat dihitung sebagai akar pangkat 2 dari 3^2 + 4^2, yaitu akar pangkat 2 dari 25, yaitu 5 cm. -
Fisika
Dalam fisika, akar pangkat 2 digunakan untuk menghitung kecepatan benda yang jatuh bebas. Rumus untuk menghitung kecepatan (v) benda yang jatuh bebas adalah v = akar pangkat 2 (2gh), di mana g adalah percepatan gravitasi dan h adalah tinggi benda dari tanah. Misalnya, jika sebuah benda jatuh bebas dari ketinggian 100 meter, maka kecepatannya saat menyentuh tanah dapat dihitung sebagai akar pangkat 2 dari 2 x 9,8 m/s^2 x 100 m, yaitu sekitar 44,3 m/s. -
Teknik
Dalam teknik, akar pangkat 2 digunakan untuk menghitung tegangan dan kuat arus dalam rangkaian listrik. Misalnya, dalam rangkaian listrik sederhana yang terdiri dari sumber tegangan (V), resistor (R), dan kapasitor (C), kuat arus (I) dapat dihitung sebagai akar pangkat 2 dari V^2 / (R^2 + C^2). Dengan memahami hubungan ini, teknisi dapat merancang dan membangun rangkaian listrik yang berfungsi dengan baik.
Aplikasi akar pangkat 2 dalam berbagai bidang ini menunjukkan pentingnya operasi matematika ini dalam dunia nyata. Akar pangkat 2 memungkinkan kita untuk memahami dan memecahkan masalah di bidang geometri, fisika, teknik, dan banyak lagi.
Sejarah
Sejarah penggunaan akar pangkat 2 sangat penting karena memberikan konteks dan pemahaman tentang perkembangan konsep matematika ini. Pengetahuan tentang akar pangkat 2 telah ada sejak zaman kuno, menunjukkan bahwa konsep ini telah menjadi bagian integral dari matematika selama berabad-abad.
Penggunaan akar pangkat 2 oleh berbagai peradaban menunjukkan pentingnya konsep ini dalam memecahkan masalah matematika dan praktis. Bangsa Babilonia kuno menggunakan akar pangkat 2 untuk menghitung diagonal persegi panjang, sementara orang Yunani menggunakannya untuk menyelesaikan masalah geometri. Matematikawan India dan Arab juga berkontribusi pada pengembangan konsep akar pangkat 2.
Dengan memahami sejarah akar pangkat 2, kita dapat mengapresiasi pentingnya konsep ini dalam perkembangan matematika dan sains. Pengetahuan tentang akar pangkat 2 dan sejarahnya memberdayakan kita untuk memahami dan menerapkan konsep ini secara efektif dalam berbagai bidang.
Rumus
Rumus (a) = |a| memiliki hubungan yang erat dengan konsep akar pangkat 2. Rumus ini menunjukkan bahwa akar pangkat 2 dari kuadrat suatu bilangan real (a) sama dengan nilai absolut dari bilangan tersebut. Artinya, akar pangkat 2 “membatalkan” operasi kuadrat.
Hubungan ini sangat penting karena memberikan pemahaman yang lebih dalam tentang sifat-sifat akar pangkat 2. Misalnya, rumus ini menjelaskan mengapa akar pangkat 2 dari bilangan positif selalu positif, karena nilai absolut dari bilangan positif selalu positif. Sebaliknya, akar pangkat 2 dari bilangan negatif selalu imajiner (mengandung satuan i), karena nilai absolut dari bilangan negatif adalah positif.
Selain itu, rumus ini juga berguna dalam menyelesaikan persamaan dan pertidaksamaan yang melibatkan akar pangkat 2. Dengan menggunakan rumus ini, kita dapat menyederhanakan persamaan dan pertidaksamaan tersebut, sehingga lebih mudah untuk diselesaikan.
Dengan demikian, rumus (a) = |a| merupakan komponen penting dari konsep akar pangkat 2. Rumus ini memberikan pemahaman yang lebih baik tentang sifat-sifat akar pangkat 2 dan membantu kita menyelesaikan masalah yang melibatkan operasi ini.
Kaitan
Akar pangkat 2 memiliki kaitan yang sangat erat dengan konsep kuadrat dan pangkat dua. Konsep kuadrat mengacu pada perkalian suatu bilangan dengan dirinya sendiri, sedangkan pangkat dua merupakan hasil dari perkalian tersebut. Akar pangkat 2, di sisi lain, merupakan operasi yang membatalkan operasi kuadrat.
Kaitan ini sangat penting karena membantu kita memahami sifat-sifat akar pangkat 2. Misalnya, akar pangkat 2 dari kuadrat suatu bilangan selalu sama dengan bilangan itu sendiri. Hal ini menunjukkan bahwa akar pangkat 2 membatalkan operasi kuadrat. Selain itu, konsep pangkat dua juga membantu kita memahami mengapa akar pangkat 2 dari bilangan positif selalu positif, karena kuadrat dari bilangan positif selalu positif.
Memahami kaitan antara akar pangkat 2 dengan konsep kuadrat dan pangkat dua sangat penting untuk menguasai operasi ini. Dengan memahami kaitan tersebut, kita dapat menggunakan akar pangkat 2 secara efektif dalam berbagai aplikasi, seperti menyelesaikan persamaan dan pertidaksamaan, serta menghitung panjang sisi miring segitiga siku-siku.
FAQ Seputar Akar Kuadrat
Berikut adalah beberapa pertanyaan umum dan jawabannya seputar akar kuadrat:
Pertanyaan 1: Apa yang dimaksud dengan akar kuadrat?
Jawaban: Akar kuadrat suatu bilangan adalah nilai yang jika dikuadratkan (dikalikan dengan dirinya sendiri) menghasilkan bilangan asal.
Pertanyaan 2: Bagaimana cara menghitung akar kuadrat?
Jawaban: Ada beberapa metode untuk menghitung akar kuadrat, salah satu yang paling umum adalah dengan menggunakan kalkulator atau tabel akar kuadrat. Cara lain adalah dengan menggunakan algoritma pembagian panjang.
Pertanyaan 3: Mengapa akar kuadrat dari bilangan negatif adalah bilangan imajiner?
Jawaban: Bilangan imajiner adalah bilangan yang mengandung satuan i, yaitu akar kuadrat dari -1. Ketika menghitung akar kuadrat dari bilangan negatif, hasilnya selalu bilangan imajiner karena tidak ada bilangan real yang jika dikuadratkan menghasilkan bilangan negatif.
Pertanyaan 4: Apa saja aplikasi akar kuadrat dalam kehidupan nyata?
Jawaban: Akar kuadrat memiliki banyak aplikasi dalam kehidupan nyata, seperti menghitung panjang sisi miring segitiga siku-siku, menghitung kecepatan benda yang jatuh bebas, dan menyelesaikan persamaan kuadrat.
Dengan memahami konsep dan aplikasi akar kuadrat, kita dapat menggunakannya secara efektif untuk menyelesaikan berbagai masalah matematika dan sains.
Beralih ke topik selanjutnya: Sifat-sifat Akar Kuadrat
Tips Menguasai Akar Pangkat Dua
Menguasai akar pangkat dua sangat penting untuk kesuksesan di bidang matematika dan sains. Berikut adalah beberapa tips untuk membantu Anda menguasai konsep ini:
Tip 1: Pahami Konsep Dasar
Sebelum mempelajari operasi akar pangkat dua, pastikan Anda memahami konsep dasar seperti kuadrat, pangkat, dan bilangan negatif.
Tip 2: Gunakan Kalkulator atau Tabel
Jika memungkinkan, gunakan kalkulator atau tabel akar kuadrat untuk mendapatkan hasil yang akurat dan cepat.
Tip 3: Latih Secara Teratur
Seperti keterampilan lainnya, menguasai akar pangkat dua membutuhkan latihan yang teratur. Kerjakan soal latihan sebanyak mungkin untuk meningkatkan kecepatan dan akurasi Anda.
Tip 4: Kuasai Sifat-sifat Akar Pangkat Dua
Pelajari dan pahami sifat-sifat akar pangkat dua, seperti sifat distributif dan sifat perkalian.
Tip 5: Terapkan dalam Konteks
Jangan hanya menghafal rumus. Cobalah terapkan akar pangkat dua dalam berbagai konteks, seperti menyelesaikan persamaan kuadrat atau menghitung panjang sisi miring segitiga siku-siku.
Dengan mengikuti tips ini, Anda dapat meningkatkan pemahaman Anda tentang akar pangkat dua dan menggunakannya secara efektif untuk memecahkan masalah matematika dan sains.
Beralih ke topik selanjutnya: Aplikasi Akar Pangkat Dua
Youtube Video:










